The point on the circle \[x^2 + y^2 + 6x +8y = 75,\] which is closest to the origin, is at what distance from the origin?
\(3\),
\(4\),
\(5\),
\(10\).
First we write the equation of this circle in its most useful form: \[(x+3)^2 + (y+4)^2 = 100.\] Now we can see that the centre of this circle is at \((-3,-4)\) and it has radius \(10\).
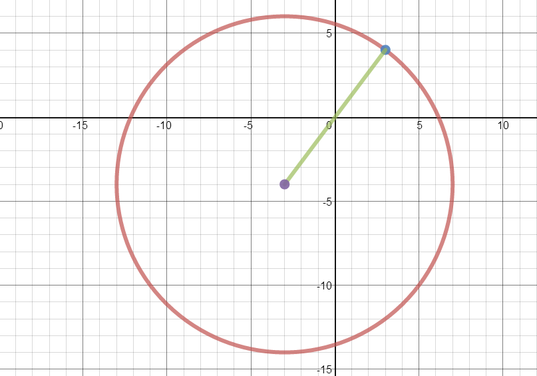
We know the point on the circle which is closest to the origin, say \(X\), lies on the line that passes through both the centre of the circle and the origin.
Are you happy with this statement? Can you see why this is true? Can we appeal to symmetry here?
The distance from the centre of the circle to \(X\) is \(10\) as it is a radius. The distance from the centre to the origin is \[\sqrt{(-3-0)^2 +(-4-0)^2}=5.\] So the closest point on the circle is at a distance of \(10-5=5\) from the origin.
So the answer is (c).

