A point \(P(x,y)\) moves so that \(OP^2=\lambda y\), where \(O\) is the origin and \(\lambda\) is a constant. Show that the locus of \(P\) is a circle. State the coordinates of the centre of the circle and the length of its radius.
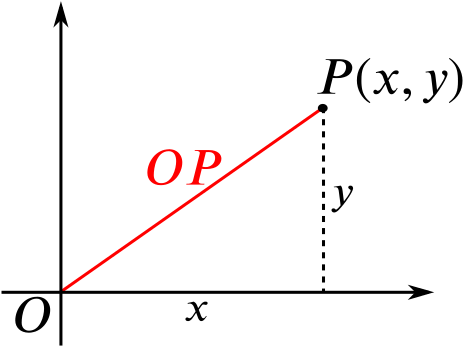
This tells us that points \(P(x,y)\) such that \(OP^2=\lambda y\) form a circle, and inspecting the equation above, we see that the circle has centre \(\left(0,\dfrac{\lambda}{2}\right)\) and radius \(\dfrac{\lambda}{2}\).
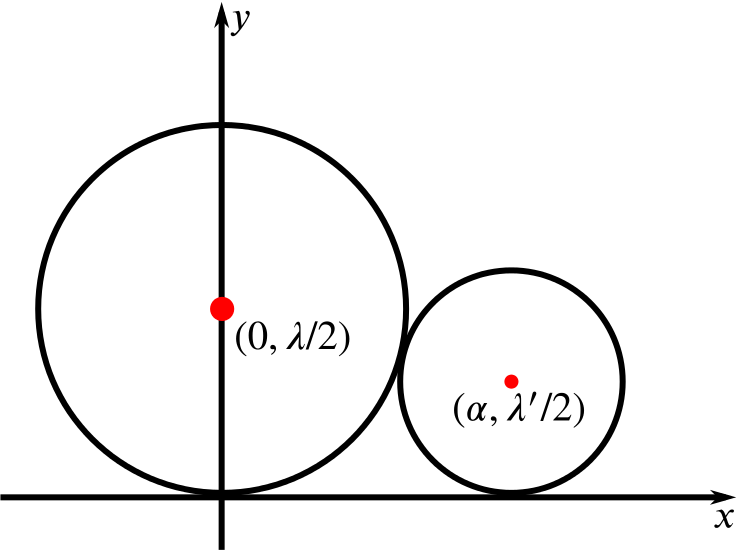
Using the same axes, find the locus of a point \(Q(x',y')\) which moves so that \(QR^2=\lambda' y'\), where \(R\) is the fixed point \((\alpha,0)\) and \(\lambda'\) is a constant.

We see the length of the base of the triangle is \(x'-\alpha\), if \(x'>\alpha\), or \(\alpha-x'\) if \(x'<\alpha\).
As squaring both of these quantities gives the same result, we see that \[\begin{align*} \lambda'y'=QR^2=(x'-\alpha)^2+y'^2 \\ (x'-\alpha)^2+\left(y'-\dfrac{\lambda'}{2}\right)^2=\dfrac{\lambda'^2}{4}, \end{align*}\]that is, such points lie on the circle with centre \(\left(\alpha,\dfrac{\lambda'}{2}\right)\), with radius \(\dfrac{\lambda'}{2}\).
If the two loci touch each other, and \(\alpha\ne 0\), prove that \(\alpha^2=\lambda\lambda'\).
There is a right-angled triangle here with side lengths that we know.
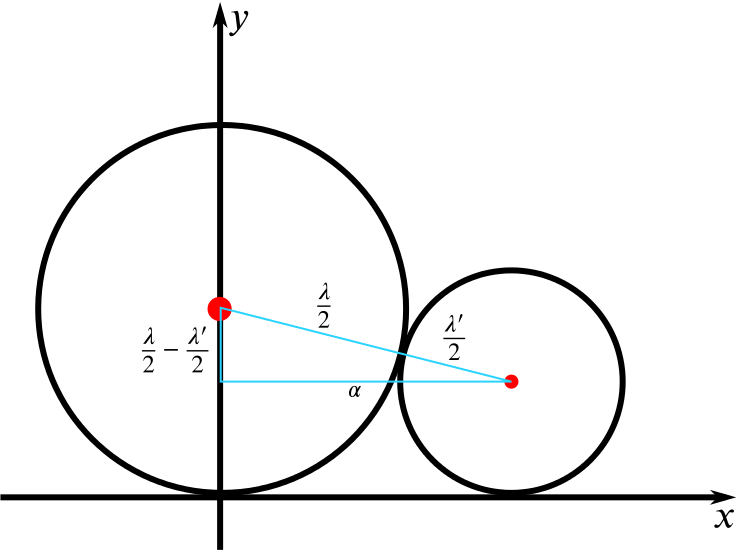
Using Pythagoras’ theorem, we find
\[ \left(\frac{\lambda}{2}+\frac{\lambda'}{2}\right)^2=\alpha^2+\left(\frac{\lambda}{2}-\frac{\lambda'}{2}\right)^2. \]
We could see this as finding (the distance between the centres of the circles\()^2\), using the formula for the distance between two points, which was originally derived from Pythagoras’s theorem.
Expanding the brackets gives
\[ \frac{\lambda^2}{4}+\frac{\lambda'^2}{4}+\frac{\lambda\lambda'}{2}=\alpha^2+\frac{\lambda^2}{4}+\frac{\lambda'^2}{4}-\frac{\lambda\lambda'}{2}. \]
Rearranging, we have that
\[ \alpha^2=\lambda\lambda'. \]

