The area bounded by the graphs \[y=\sqrt{2-x^2} \qquad \text{and} \qquad x+\left(\sqrt{2}-1\right)y=\sqrt{2}\] equals
- \(\dfrac{\sin{\sqrt{2}}}{\sqrt{2}}\);
- \(\dfrac{\pi}{4}-\dfrac{1}{\sqrt{2}}\);
- \(\dfrac{\pi}{2\sqrt{2}}\);
- \(\dfrac{\pi^2}{6}\).
The equation \(y=\sqrt{2-x^2}\) can be squared to get \(y^2=2-x^2\), or \(x^2+y^2=2\). This is a circle centred at the origin with radius \(\sqrt{2}\).
The original equation, though, is \(y=\sqrt{\vphantom{x^2}\cdots}\), which is never negative, so we actually only have the semicircle with \(y\ge0\).
The graph of \(x+\left(\sqrt{2}-1\right)y=\sqrt{2}\) is a straight line which intersects the \(y\)-axis at \(\left(0, 2+\sqrt{2}\right)\), and the \(x\)-axis at \(\left(\sqrt{2},0\right)\), which is on the circumference of the circle.
We can now sketch these two graphs.
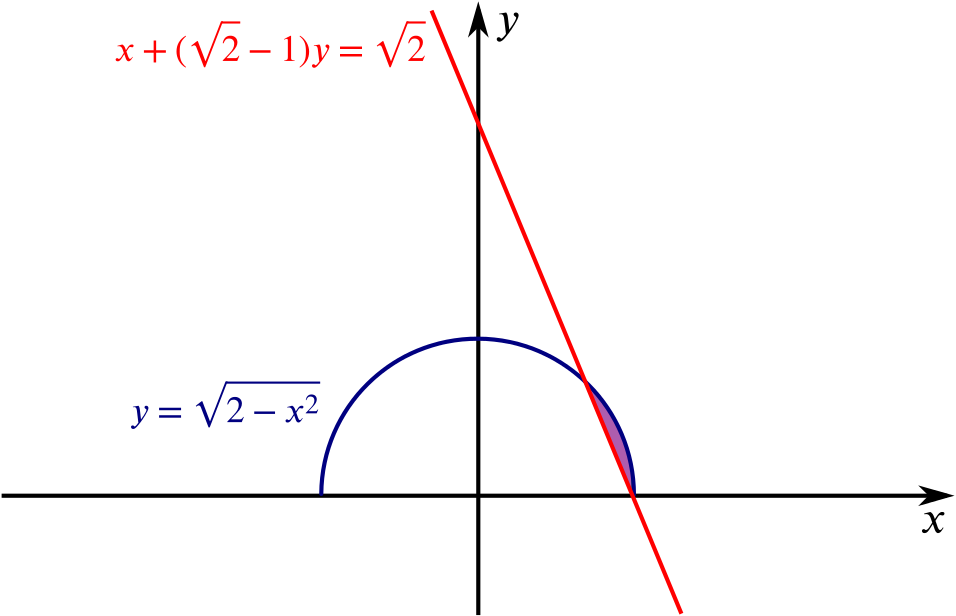
To find the other point of intersection, we substitute \(x=\sqrt{2}-\left(\sqrt{2}-1\right)y\) into the equation of the circle, to get \[\begin{gathered} \left(\sqrt{2}-\left(\sqrt{2}-1\right)y\right)^2+y^2=2\\ \implies\quad 2-2\sqrt{2}\left(\sqrt{2}-1\right)y+\left(\sqrt{2}-1\right)^2y^2+y^2=2\\ \implies\quad 2-\left(4-2\sqrt{2}\right)y+\left(3-2\sqrt{2}\right)y^2+y^2=2\\ \implies\quad -\left(4-2\sqrt{2}\right)y+\left(4-2\sqrt{2}\right)y^2=0\\ \implies\quad \left(4-2\sqrt{2}\right)y(-1+y)=0. \end{gathered}\] So \(y=0\) (the intersection we already know about) or \(y=1\).
Alternatively, substituting \(y=\sqrt{2-x^2}\) into the equation of the line gives a shorter solution if we notice that \(2-x^2 = \left(\sqrt{2}-x\right)\left(\sqrt{2}+x\right)\).
So the line intersects this semicircle at \(\left(\sqrt{2},0\right)\) and \((1,1)\).
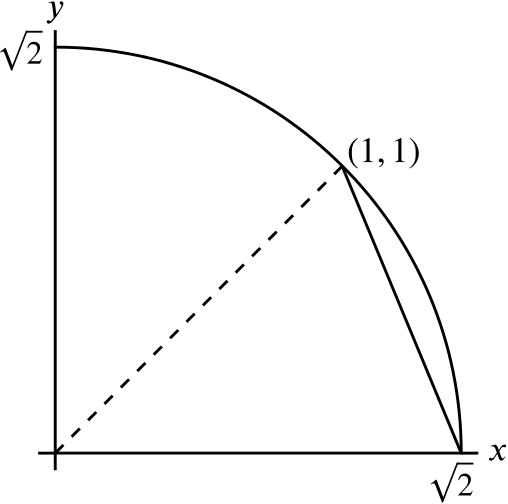
The sector has an angle of \(45^\circ=\dfrac{\pi}{4}\). The simplest way to calculate the area of this segment is to work out the area of \(\frac{1}{8}\) of the circle, and then subtract the triangle which has base \(\sqrt{2}\) and height \(1\).
So the area is \[\frac{1}{8} \times 2\pi - \frac{1}{2} \times \sqrt{2} \times 1 = \frac{\pi}{4} - \frac{1}{\sqrt{2}}\]
and the answer is (b).
Once we know that the area we seek is the difference between the area of a sector of a circle and the area of a triangle, does one of the answers pick itself?

