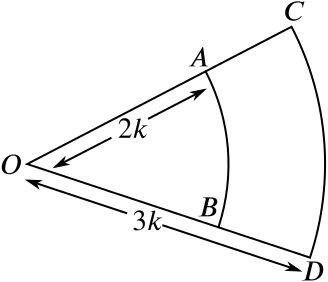
The figure shows two sectors in which \(AB\), \(CD\) are arcs of concentric circles, centre \(O\) and radii \(\quantity{2k}{cm}\) and \(\quantity{3k}{cm}\) respectively. The angle \(A\hat{O}B\) is \(\dfrac{3}{4}\) radian and the area \(ABDC\) is \(\quantity{30}{cm^2}\). Find
- the value of \(k\),
The area of a sector with radius \(r\) containing an angle \(\theta\) is \(A=\dfrac{1}{2}r^2\theta\). Hence the difference in the sector areas \(30 = \dfrac{1}{2}(3k)^2\dfrac{3}{4} - \dfrac{1}{2}(2k)^2\dfrac{3}{4}\).
Solving this for \(k\) gives \(k=4\).
Find
- the difference between the lengths of the arcs \(AB\) and \(CD\).
The length of an arc of radius \(r\) and given by an angle \(\theta\) is \(r\theta\). Hence the difference between arc \(AB\) and arc \(CD\) is \(12\times\dfrac{3}{4} - 8\times\dfrac{3}{4} = \quantity{3}{cm}\).

