The point on the circle \[(x-5)^2+(y-4)^2=4\] which is closest to the circle \[(x-1)^2+(y-1)^2=1\] is
- \((3.4,2.8)\),
- \((3,4)\),
- \((5,2)\),
- \((3.8,2.4)\).
Here is a diagram of the circles:
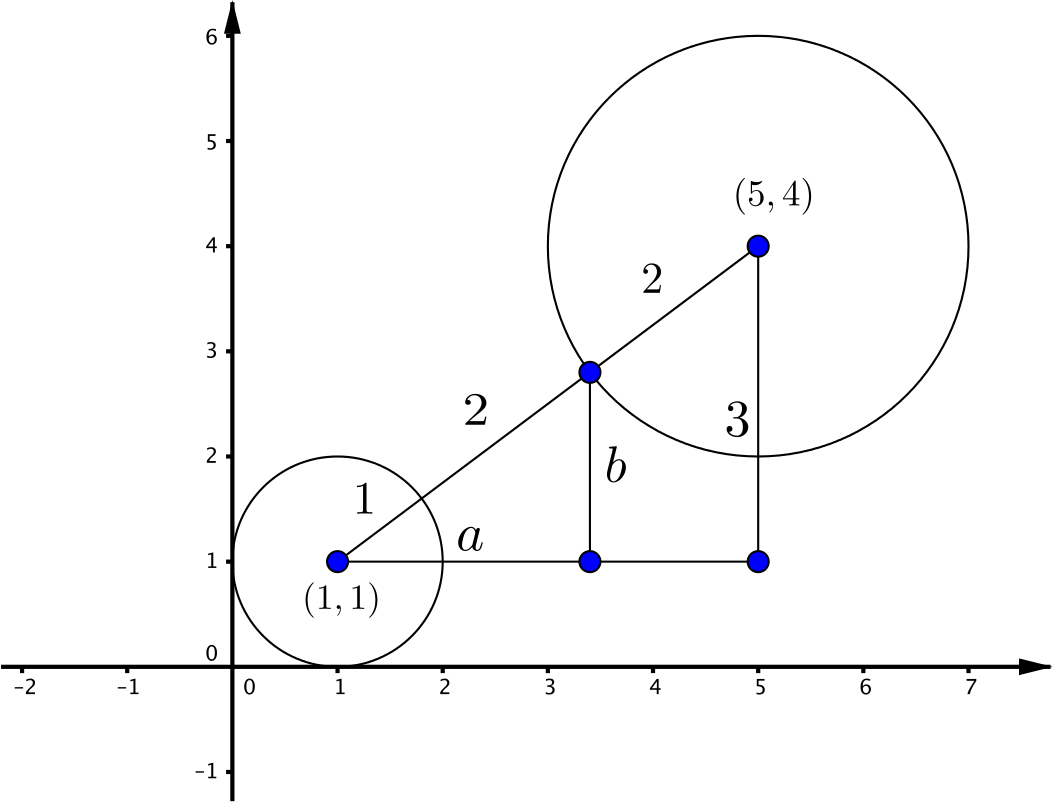
Approach 1
The right-angle triangle with the circle centres at two of its vertices has sides of length \(3\) and \(4\). Its hypotenuse is therefore of length \(5\).
Using similar triangles, we have \(\dfrac{3}{5}=\dfrac{a}{4}=\dfrac{b}{3}\). Thus \(a = 2.4, b = 1.8\), and the point on the first circle closest to the second is \((3.4,2.8)\). The answer is (a).
Approach 2
The vector joining \((5,4)\) and \((1,1)\), the centres of the circles, is \(\begin{pmatrix}-4\\-3\end{pmatrix}\). The length of this vector is \(\sqrt{(-4)^2+(-3)^2}=5\).
The first circle has radius \(2\), and so the point on this closest to the second is \(\dfrac{2}{5}\)ths of the way along this vector. Hence we can calculate the point: \[\begin{pmatrix}5\\4\end{pmatrix} + \frac{2}{5}\begin{pmatrix}-4\\-3\end{pmatrix} = \begin{pmatrix}5\\4\end{pmatrix} + \begin{pmatrix}-1.6\\-1.2\end{pmatrix} = \begin{pmatrix}3.4\\2.8\end{pmatrix}.\]
Therefore the answer is (a).

