The fixed points \(A\) and \(B\) have coordinates \((-3a,0)\) and \((a,0)\) respectively. Find the equation of the locus of a point \(P\) which moves in the coordinate plane so that \(AP=3PB\). Show that the locus is a circle, \(S\), which touches the axis of \(y\) and has its centre at the point \(\left(\dfrac{3}{2}a,0\right)\).
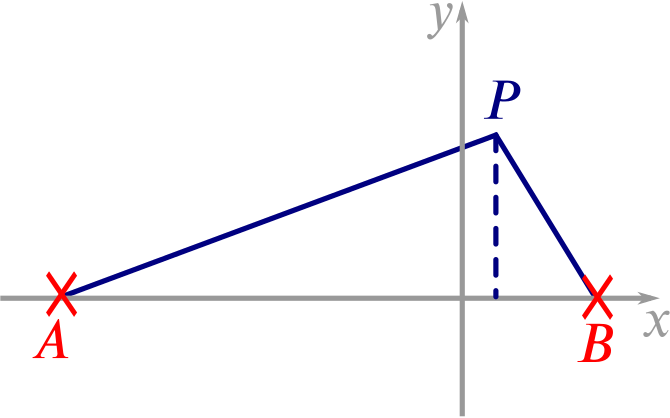
Let \(P=(x,y)\). Then \(AP=\sqrt{(x+3a)^2+y^2}\) and \(PB=\sqrt{(x-a)^2+y^2}\). We want \(P\) to satisfy \[AP=3PB,\] so the equation for the locus of \(P\) is given by \[\sqrt{(x+3a)^2+y^2}=3\sqrt{(x-a)^2+y^2}.\] Squaring both sides, we find that \[x^2+6ax+9a^2+y^2=9x^2-18ax+9a^2+9y^2,\] which simplifies to \[8x^2-24ax+8y^2=0,\] and so the locus of \(P\) is \[x^2-3ax+y^2=0.\] Writing this in the form of an equation of a circle \[\left(x-\dfrac{3a}{2}\right)^2+y^2=\left(\dfrac{3a}{2}\right)^2,\] which is a circle centred at \(\left(\dfrac{3a}{2},0\right)\) of radius \(\dfrac{3a}{2}\), which touches the \(y\) axis (since putting \(x = 0\) gives a single value for \(y\)).
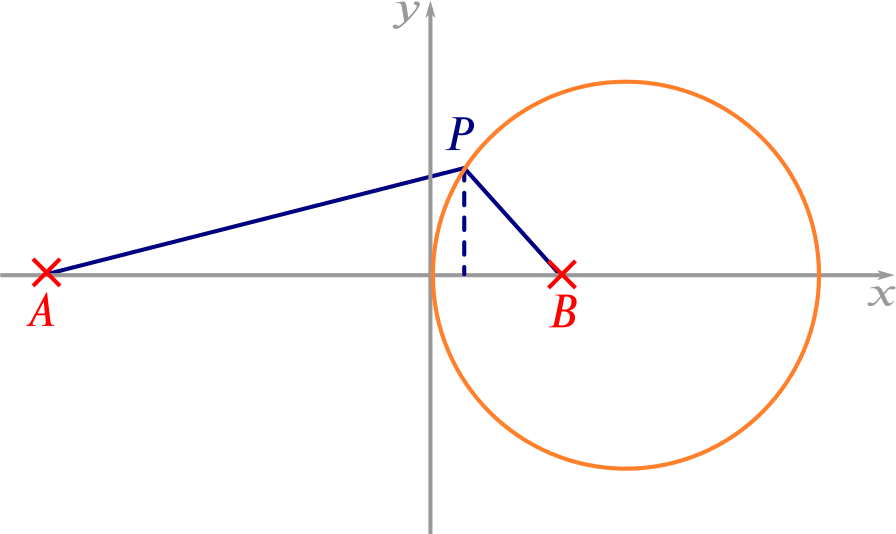
A point \(Q\) moves in such a way that the perpendicular distance of \(Q\) from the axis of \(y\) is equal to the length of a tangent from \(Q\) to the circle \(S\). Find the equation of the locus of \(Q\).
You might have noticed that there are two possible tangents we could have drawn from \(Q\) to the circle \(S\). How do we know that we would get the same answer if we used the other tangent?
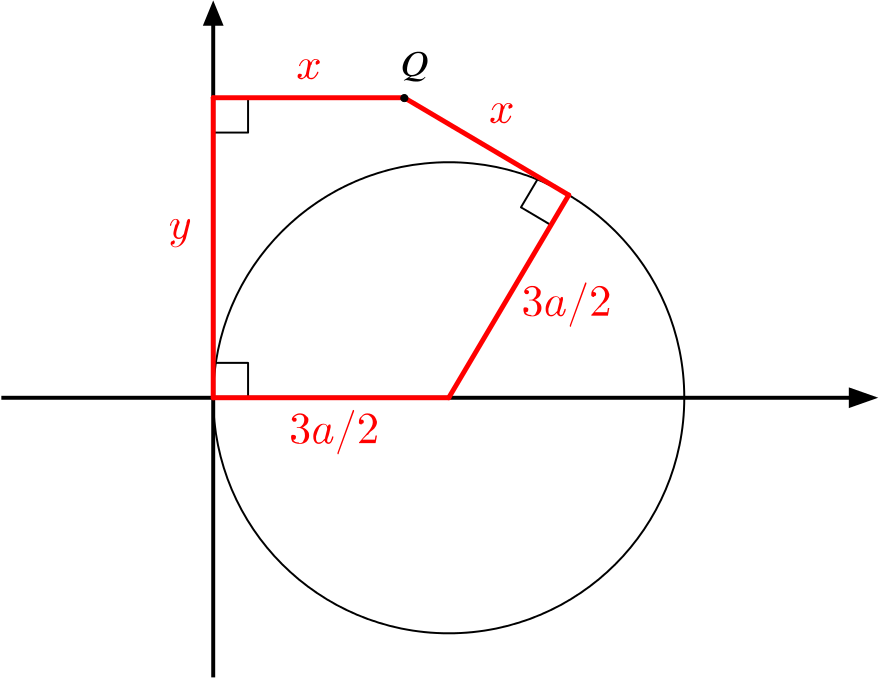
We’ll consider the shape formed by the sides whose lengths we already know (in red above).
Let the length of the hypotenuse of the right-angled triangle with side-lengths \(x\) and \(\dfrac{3a}{2}\) be \(d\), and so
\[\begin{equation} d^2=x^2+\left(\frac{3a}{2}\right)^2.\label{eq:1} \end{equation}\]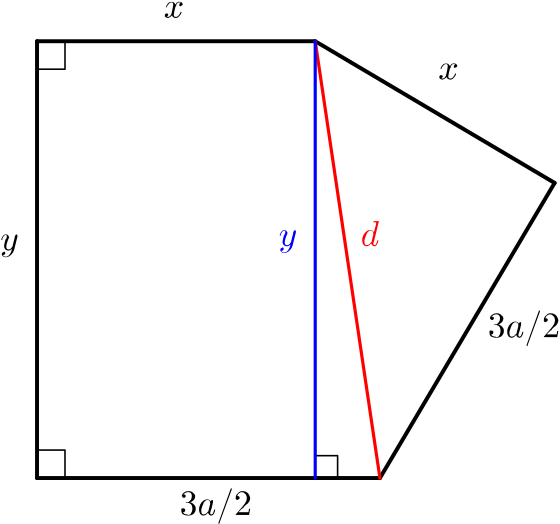
We now add an additional vertical line.
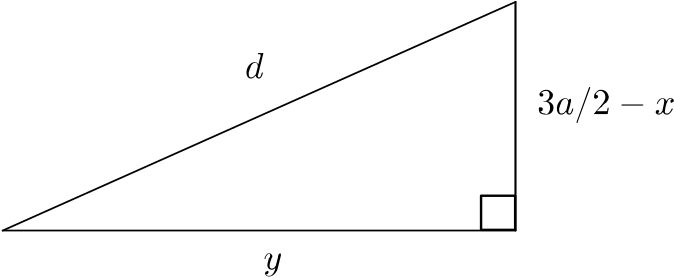
Using Pythagoras’ Theorem and \(\eqref{eq:1}\), we have that
\[\begin{align*} d^2 &=\left(\frac{3a}{2}-x\right)^2+y^2 \\ \Longrightarrow \quad x^2+\left(\frac{3a}{2}\right)^2 &=\left(\frac{3a}{2}-x\right)^2+y^2 \\ \Longrightarrow \quad x^2+\left(\frac{3a}{2}\right)^2 &=\left(\frac{3a}{2}\right)^2-3ax+x^2+y^2 \\ \Longrightarrow \quad y^2&=3ax, \end{align*}\]and so the equation of the locus of \(Q\) is \(y^2=3ax\).
If we drew \(Q\) with a negative \(y\)-coordinate on our original diagram, would we have the same answer?
What if the \(x\)-coordinate was greater than \(3a\)?
Do we need to consider either of these cases separately, or can they be deduced from the case we have already done?
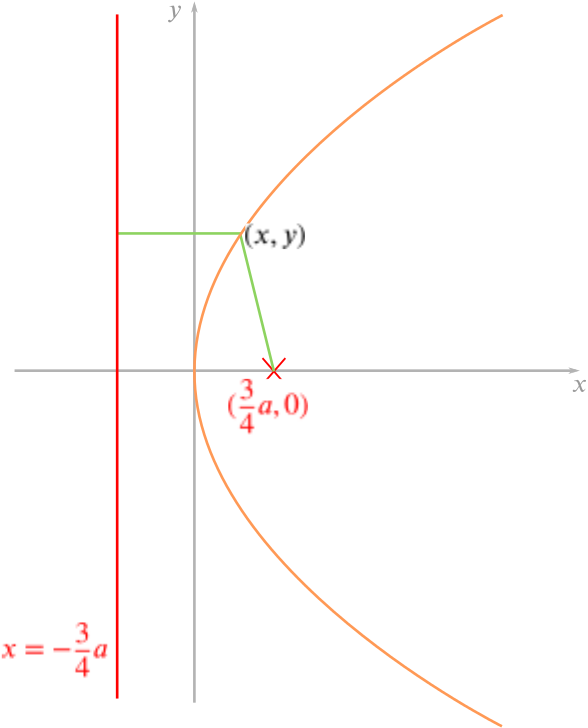
Show that this locus is also the locus of points which are equidistant from the line \(4x+3a=0\) and the point \(\left(\dfrac{3}{4}a,0\right)\).
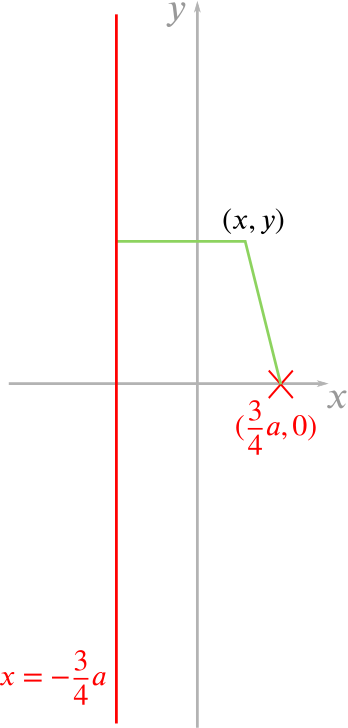
We have that the distance of a point \((x, y)\) from the line \(4x+3a=0\) is \(x+\dfrac{3a}{4}\), and the distance from the same point \((x,y)\) to \(\left(\dfrac{3a}{4},0\right)\) is \(\sqrt{\left(x-\dfrac{3a}{4}\right)^2+y^2}\).
Setting these equal to each other and squaring both sides, we have that \[x^2+\dfrac{3ax}{2}+\dfrac{9a^2}{16}=x^2-\dfrac{3ax}{2}+\dfrac{9a^2}{16}+y^2.\] Cancelling, we find that the locus of points equidistant from the line \(4x+3a=0\) and the point \(\left(\dfrac{3a}{4},0\right)\) is \[y^2=3ax,\] which is the same locus that we found previously.