We often think of functions in terms of numbers and algebraic expressions, such as \(f(x) = 2x\), and the graphs we can draw of them. But really the concept of a function is much more universal. And it can be easier to understand some of a function’s basic features using a simpler example.
Imagine you have brought back some presents from holiday for your friends. To make sure everyone gets what they like, you make a list of the various presents, a list of your friends’ names, and draw an arrow from a present to a friend if you think that would be a good match. This allocation of presents to people is an example of a function. The domain of the function consists of the presents and the range consists of your friends.
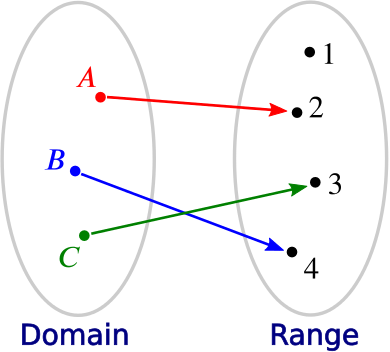
But you soon discover that not any old function will do. You definitely wouldn’t want to leave anyone out; each friend should receive at least one present. What you are looking for is a function that is surjective (or onto): for every element of the range (every friend) there should be at least one element of the domain (one present) that gets allocated to them.
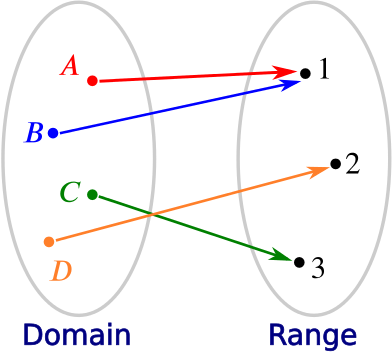
You also decide that no one should get more than one present, as that would be a bit much. So you also need your function to be injective (or one-to-one): for every element of the range (every friend) there should be no more than one element of the domain (one present) that gets allocated to it.
|
|
What you’re looking for, then, is a function that is both injective (one-to-one) and surjective (onto)—and there is a name for that too. A function that is both injective and surjective is called a bijection. It gives you an exact correspondence between elements of the domain and the range: exactly one present for each person.
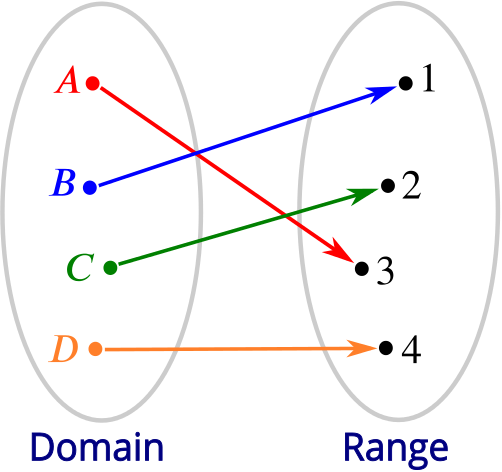
Given a finite list of presents (a domain) and friends (a range), can you always find a bijection between the two? The answer is no.
If there is to be exactly one present for each friend, there have to be as many presents as friends: the domain has to contain the same number of elements as the range. Conversely, if the domain and range contain the same number of elements, then you can be sure that there is a bijection.
One thing that is important to notice is that whether a function is injective, surjective or bijective depends on how you define the domain and range. Imagine that after having carefully constructed a bijection between your presents and your friends, you suddenly notice that you have forgotten someone. Adding this someone to your list of friends (exchanging the range) immediately ruins your bijection, as there isn’t a present for that new friend. The function you are left with is still injective, but not surjective.
Similarly, if instead of finding an extra friend you find an extra present in your bag and allocate it to someone (you extend the domain), then your function is no longer injective, as someone will now get two presents.
Therefore, when we are checking whether a function is injective, surjective or both, we need to be very clear about its domain and range. That goes not only for friends and presents, but also for more mathematical examples, such as the function \(f(x)=2x\). Suppose we define the domain and the range to consist of all the natural numbers \(1\), \(2\), \(3\), …. To show that the function is injective, we need to show that no two distinct natural numbers \(x_1\) and \(x_2\) in the domain are allocated to the same number \(y\) of the range. This is clearly the case, since if \(x_1\) and \(x_2\) are distinct, then so are \(2x_1\) and \(2x_2\).
To show that the function is surjective, we need to show that for every real number \(y\) in the range, there is a real number \(x\) in the domain that is allocated to it. This number would clearly have to be \(y/2\). But if \(y\) is odd, then \(y/2\) is not a natural number, so there isn’t an element of the domain that is allocated to it. Therefore, the function is not surjective.
We can remedy this situation by changing the range to consist only of the even natural numbers. In this case, the function is a bijection.

