Are there more irrational numbers than rational numbers, or more rational numbers than irrational numbers? Well, there are infinitely many of both, so the question doesn’t make sense. It turns out, however, that the set of rational numbers is infinite in a very different way from the set of irrational numbers: it’s countable.
In mathematics, an infinite set is called countable if its members can be listed in some order: the 1st one is \(a\), the 2nd one is \(b\), the 3rd one is \(c\), and so on.
For example, the integers are countable, as we can list them as follows:
1st: \(0\)
2nd: \(1\)
3rd: \(-1\)
4th: \(2\)
5th: \(-2\)
6th: \(3\)
7th: \(-3\)
and so on. Every integer will appear somewhere in this list.
In 1873, Georg Cantor showed that we can do the same for the rational numbers. This is one way to achieve this. We draw a table with all of the rational numbers, as follows:
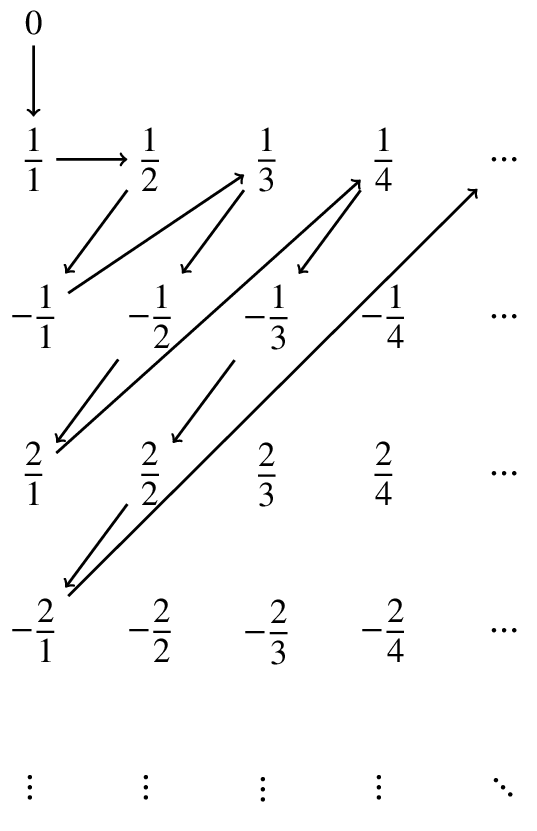
In this table, the 1st row has numerator \(0\), the 2nd row has numerator \(1\), the 3rd row has numerator \(-1\), and so on, following the order that we used above. The \(n\)th column has denominator \(n\) for each \(n\). Then by following the zig-zag line, starting from \(0\), we reach every single possible rational number, so we can list them. (Some fractions are not in simplest form; we simply ignore these when writing down our list, as their simplest form equivalents will appear earlier in the list.) So the rational numbers are also countable!
The same isn’t true of the irrational numbers: they form an uncountably infinite set. In 1873, Cantor also came up with a beautiful and elegant proof of this fact.
We’ll start by showing that the real numbers are uncountable. We will prove this by contradiction, so let’s suppose the real numbers are countable. This means that we can make a list of them, for example
- \(0.1234567\dots\)
- \(1.4367892\dots\)
- \(2.3987851\dots\)
- \(3.7891234\dots\)
- \(4.1415695\dots\)
and so on, with every real number occurring somewhere in the infinite list. Now take the first digit after the decimal point of the first number, the second digit after the decimal point of the second number, the third digit after the decimal point of the third number, and so on, to get a new number \(0.13816\dots\).
Now change each digit of this new number, for example by changing every digit which is not a \(1\) into a \(1\), but every \(1\) into a \(2\). This gives the new number \(0.21121\dots\). This new number is not the same as the first number on the list, because their first decimal digits are different. Neither is it the same as the second number on the list, because their second decimal digits are different. Carrying on like this shows that the new number is different from every single number on the list, and so it cannot appear anywhere in the list.
But we started with the assumption that every real number was on the list! The only way to avoid this contradiction is to admit that the assumption that the real numbers are countable is false. Therefore, the real numbers are uncountable – there really are more of them than there are rational numbers!
It also follows from this that the irrational numbers themselves are uncountable. For when we put the rational numbers and the irrational numbers together we get all the real numbers: each number on the line is either rational or irrational. If the irrational numbers were countable, just as the rationals are, then the real numbers would be countable too—it’s not too hard to convince ourselves of that. So the irrational numbers themselves are uncountable.
So we have two different infinities: the number of rationals or integers and the number of irrational numbers.
Cantor went on to define all sorts of other infinities too, each one bigger than the next, with the countable infinity at the bottom of the hierarchy. When he first published these ideas, Cantor faced strong opposition from some of his colleagues. One of them, Henri Poincaré, described Cantor’s ideas as a “grave disease” and another, Leopold Kronecker, went so far as to denounce Cantor as a “scientific charlatan” and “corrupter of youth”. Cantor suffered severe mental health problems which may have been exacerbated in part from the rejection his work had met with. But we now know that his work had simply come too soon: by 30 years on, Cantor’s ideas were forming a central pillar of mathematics, and many of his results can be found in standard textbooks today.

