We’ll start with two examples.
Imagine trying to balance this spoon on your finger. What would happen if your finger were near \(A\)? What it were near \(B\) instead?

Your finger would act as a pivot and can be placed at any point on the spoon between \(A\) and \(B\), but the behaviour of the spoon (whether it will stay balanced or the direction in which it will rotate about the pivot) depends on the position of the pivot. Imagine how the spoon would behave for each position of the pivot between \(A\) and \(B.\) At some point between \(A\) and \(B\), the direction in which the spoon would rotate changes. This is the balancing point.
Now think about the quadratics \(x^2-2x-1\), \(x^2-2x+1\), and \(x^2-2x+3.\) These are all of the form \(x^2-2x+c\), but what happens to the roots as \(c\) varies continuously? Can you visualise this? In Discriminating we explore how and why the discriminant determines the number of roots of a quadratic, thinking algebraically and graphically.
These examples both involve some sort of limiting behaviour in a system where something can vary continuously. In the first case, there is a limit point where the direction in which the spoon will topple changes. In the quadratic example, there is a value of \(c\) for which the quadratic changes from having \(2\) distinct real roots to \(2\) distinct complex roots (i.e. \(0\) real roots ). As \(c\) approaches this value, the two roots move closer together until they coincide.
A limiting circle theorem offers a geometric example of limits. The GeoGebra interactive in the resource allows you to explore what would happen if points in this diagram were moved.

For example, what can you say about the angle at \(D\) if \(D\) moves round the circle and all other points stay fixed? What can you say about the angle \(\theta\) as \(D\) approaches \(B\) along the circle? What about the chord \(BD\)? What happens to the angle at \(D\) if \(D\) moves outside the circle or inside the circle? This geometric approach to limits enables us to make connections between results about circles.
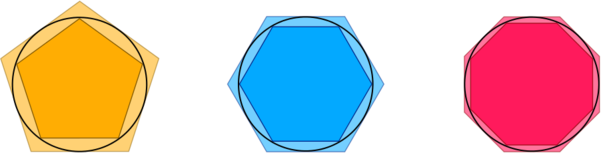
Another ancient example of limiting behaviour is Archimedes’ approximation of \(\pi\), achieved by constructing regular polygons with more and more edges inside and around a circle. You can read more about this in Pinning down \(\pi\).
There are many places in mathematics where we ask what happens as something gets very close to something else, or as it gets very small or very large, or what happens as something goes on ‘for ever’. This brings together ideas of limits and infinity. The notion of infinity intrigues people and in mathematics we sometimes try to pin it down, sometimes avoid it, sometimes find ways to circumnavigate it, and sometimes embrace it. As the mathematics educator Caleb Gattegno famously said, mathematics is ‘shot through with infinity’ and it is a useful exercise to take note of the appearance of the infinite throughout mathematics.
Given an infinite sequence, such as \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5},...\) we might wonder whether the terms eventually get as close as we like to some particular number. If this happens, then we say the sequence has a limit or tends to a limit or converges.
We might also consider what happens if we add up the terms in an infinite sequence. Under certain conditions, this sum can be finite — think about \(3+0.3+0.03 +0.003+\dotsm\) for example. Zeno’s paradox of Achilles and the tortoise is about grappling with this idea and the resource Square spirals offers a geometric way to visualise such situations.

As well as analysing how sequences and series behave, we might be interested in how they were generated in the first place. Bouncing to nothing concerns a sequence generated by a bouncing ball. The height reached on each bounce is \(\frac{3}{4}\) of the height reached on the previous bounce. Now think about how you can generate the Fibonacci sequence. The first two terms, \(0\) and \(1\), are added together to produce the next term, \(1.\) Then we add the \(1\) and \(1\) to get \(2\), we add the (second) \(1\) and the \(2\) to get \(3\), and so on. Notice that in both these examples an action is being repeated, but each time we are acting on the previous outputs. This is referred to as iteration. Iteration doesn’t have to go on for ever — for example, you can factorise a large number \(N\) by looking for the smallest factor \(f\), and then applying the same action to \(\tfrac{N}{f}\) until \(\tfrac{N}{f}\) reaches \(1.\) In other cases, the process continues for ever, producing infinite sequences that may be divergent, constant, or oscillating. Iteration is particularly important when it produces a convergent sequence with an identifiable limiting value. Staircase sequences and Staircase sequences revisited explore sequences of rational numbers, such as the one below, whose limit is an irrational number.

We can extend the idea of limits of sequences to functions and ask what happens to the function \(f(x)\) as \(x\) approaches some particular value, or we might consider what happens to the value of \(f(x)\) as \(x\) tends to infinity. For example, how does \(\frac{1}{x}\) behave as \(x\) approaches \(0\)? How does it behave as \(x\) tends to infinity? Picture the process I also relates the behaviour of functions to physical processes. Thinking about what happens as a process continues over time provides a further way to make connections between the model and the process. For example, as a cup of tea cools down in a room of constant temperature, the temperature of the tea gets closer and closer to the room temperature, say \(20^{\circ}\)C, and a graph of this would have an asymptote \(y=20.\) You can think more about asymptotes by working on Approaching asymptotes or Can you find … asymptote edition in which we ask for an equation of a function which behaves as shown below.

If we know how two functions behave as we approach a particular value, then we might be interested in how combinations such as their sum, product or quotient behave. One famous example is to ask what happens to \(\dfrac{\sin \theta}{\theta}\) as \(\theta\) tends to \(0.\) Do you think this approaches a limit? Is the quantity even defined?

In the diagram above, arc \(AB\) has length \(\theta\) and this is sandwiched between line segments of length \(\sin \theta\) and \(\tan \theta\), so we have \(\sin \theta \leq \theta \leq \tan \theta.\) This inequality can be manipulated to obtain \(\cos \theta \leq \dfrac{\sin \theta}{\theta} \leq 1.\) As \(\theta \rightarrow 0\), \(\cos \theta \rightarrow 1\) so \(\dfrac{\sin \theta}{\theta}\) is squeezed between \(1\) and a quantity whose limit is \(1.\) Therefore \(\dfrac{\sin \theta}{\theta}\rightarrow 1\) as \(\theta \rightarrow 0.\)
This result is an example of an underlying idea in calculus, where we embrace the infinite by understanding that when quantities become infinitesimally small, their relative behaviour is interesting. For example, we can find the gradient of a curve by taking a sequence of chord gradients from a point and making the chords shorter and shorter. The ‘rise’ and the ‘run’ approach zero as the chords get shorter, so you might think that the gradient is approaching \(\frac{0}{0}\), whatever that might mean. But, as in the example of \(\frac{\sin \theta}{\theta}\) above, we are looking at their relative behaviour rather than the absolute behaviour of each part of the fraction and we are therefore able to say that the gradient approaches some limit that is finite. Another way to see this limit is by Zooming in to a particular point on a curve. As you zoom in, you can see how the curve looks more and more like a straight line, or the tangent to the curve at that point.
In a number of resources, such as What else do you know? and Slippery slopes, we ask you to consider integrals or derivatives of functions which can be obtained by transforming other functions. Being able to do this depends on certain limits ‘behaving well’ or responding to the transformation in the way the function itself does. You might like to go back to the limit definition of a derivative or think about zooming in to explain why the gradient function of \(3f(x)\) is \(3f’(x).\)
As well as considering graph transformations or limits of gradients of chords, we can obtain derivatives using geometric arguments. For example, in Similar derivatives we observe that in the following diagram, \(\triangle PTS\) is similar to \(\triangle OTQ\) and therefore \(\triangle PTS\) and \(\triangle OPQ\) get closer and closer to being similar as \(\delta \theta \rightarrow 0\). This observation enables us to obtain derivatives of trigonometric functions such as \(\tan \theta\) and \(\sec \theta\) using geometric arguments.

We also embrace the infinite in calculus by coming to the amazing conclusion that you can sum slices of areas and volumes on infinitesimally small intervals to make something finite, and get ‘true’ finite results that we cannot calculate in the finite world. You can explore this in Cutting spheres where the surface area of a sphere is calculated by considering very thin parallel slices.

As well as being a subject of study in their own right, thinking about limits can be used as an approach to solving problems. By thinking about what would happen if we took something to an extreme, we might be able to make sense of the problem or determine whether a statement or conjecture is plausible.
Limits is one of the ideas that we have chosen to highlight in our pervasive ideas.

