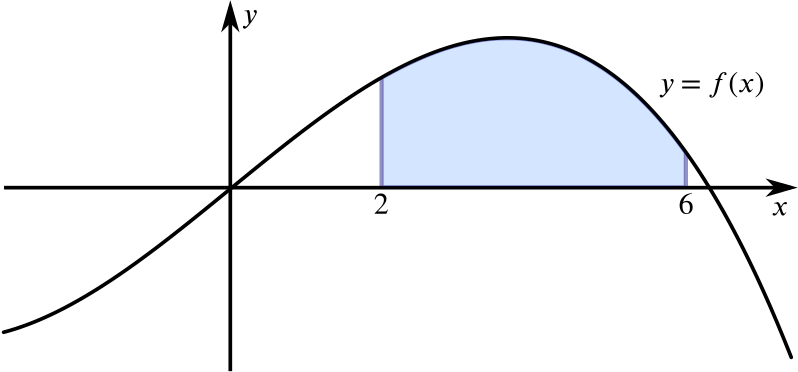
If you know that the area of the shaded region is 40 square units, which of the following can you evaluate?
\(\int_2^6 (f(x) + 5) \ dx\)
\(\int_2^6 (f(x) - 3) \ dx\)
\(\int_0^4 f(x + 2) \ dx\)
\(\int_2^6 f(x + 2) \ dx\)
\(\int_4^8 f(x + 2) \ dx\)
\(\int_2^6 -f(x) \ dx\)
\(\int_2^6 f(-x) \ dx\)
If there are any that you cannot evaluate, what additional information would you need in order to do so?
Can you find the value of the constant \(k\) for which
\[\int_2^6 (f(x) + k) \ dx = 0\]
How does your thinking change if instead you start with this image, in which the shaded area is 8 square units?

Which of the integrals above can you evaluate for the linear function \(g(x)\)?
How does this compare to your answer for \(f(x)\)?
What makes this function different from \(f(x)\)?
What else do you know about \(g(x)\)?

