How does your thinking change if instead you start with this image, in which the shaded area is 8 square units?

Which of the integrals above can you evaluate for the linear function \(g(x)\)?
A summary of the integrals and their values is provided below:
| Integral | Value |
|---|---|
| \(\int_2^6 g(x) + 5 \ dx\) | \(28\) |
| \(\int_2^6 g(x) - 3 \ dx\) | \(-4\) |
| \(\int_0^4 g(x + 2) \ dx\) | \(8\) |
| \(\int_2^6 g(x + 2) \ dx\) | \(12\) |
| \(\int_4^8 g(x + 2) \ dx\) | \(16\) |
| \(\int_2^6 -g(x) \ dx\) | \(-8\) |
| \(\int_2^6 g(-x) \ dx\) | \(-8\) |
- How does this compare to your answer for \(f(x)\)?
It is possible to evaluate all of the integrals for \(g(x)\) whereas for \(f(x)\) it was only possible to evaluate four of them.
What other integrals can we evaluate for \(g(x)\)?
What makes this function different from \(f(x)\)?
What else do you know about \(g(x)\)?
Starting with the obvious, the graph of \(y=g(x)\) is a straight line whereas the graph of \(y=f(x)\) is not. What this means is that we actually know a lot more about the behaviour of \(g(x)\) compared to \(f(x)\).
\(g(x)\) can be written in the form \(ax + b\) and from the diagram we can see that \(b=0\).
\(g(x)\) has rotational symmetry about the origin.
- \(g(x)\) has a constant gradient, \(a\). This means that we can write \[a = \dfrac{y_{1}}{2} = \dfrac{y_{2}}{6},\] where \(y_{1}\) and \(y_{2}\) are the \(y\)-values when \(x=2\) and \(x=6\) respectively. Rearranging we have that \[\begin{equation} 3y_{1} = y_{2}. \label{eq:1} \end{equation}\]
- We know that the shaded area in the diagram is a trapezium so we can therefore write \[8 = \frac{1}{2}(y_{1} + y_{2}) \times 4 = 2(y_{1} + y_{2}).\] Rearranging we have that \[\begin{equation} y_{1} + y_{2} = 4. \label{eq:2} \end{equation}\]
Solving \(\eqref{eq:1}\) and \(\eqref{eq:2}\) simultaneously we find that \(y_{1}=1\) and \(y_{2}=3\). Substituting this back into the equation for the line we have that \[y=g(x) = \dfrac{1}{2}x.\]
Now that we know the function \(g(x)\) we are able to evaluate all of the integrals. We can use this to identify important, previously unknown values such as for \(\int_2^6 g(x + 2) \ dx\) as shown below.
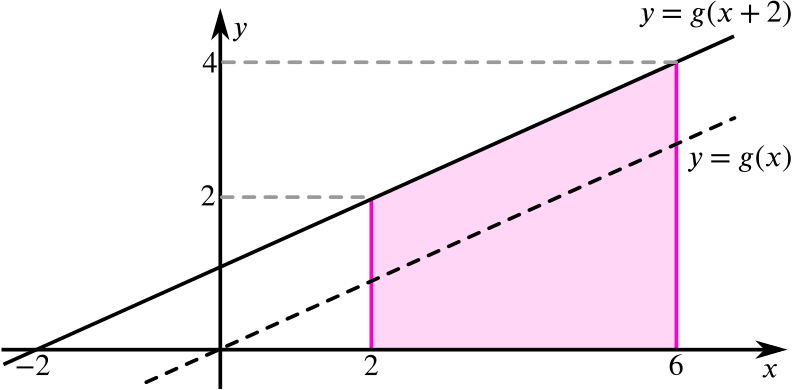
Identifying the equation of the straight line allows us evaluate all of the specified integrals, and indeed any other integral that we may choose. However, it is worth noticing that, in comparison to the non-linear function \(f(x)\), we can still evaluate many more integrals without this information.
For instance, consider how you might evaluate the integral \(\int_2^6 g(8 - x) \ dx\) without knowing the function \(g(x)\).

