Here are the graphs of four functions. The equations of the graphs are \[y=f(x) \quad y=f(x)-8 \quad y=3f(x) \quad \text{and} \quad y=3f(x)+8.\]
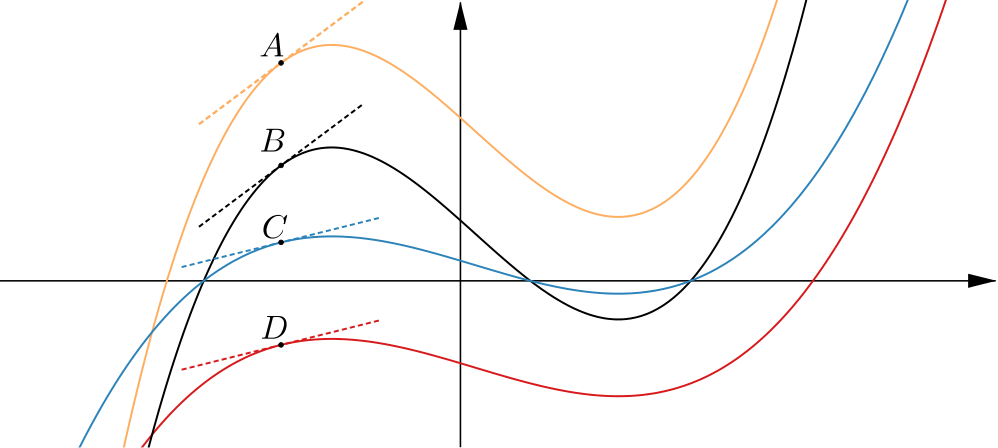
The \(x\)-coordinates of \(A\), \(B\), \(C\) and \(D\) are all the same. What can you deduce about the gradients of the curves at \(A\), \(B\), \(C\) and \(D\)?
The gradient of the tangent at \(D\) is \(\tfrac{1}{4}\). What are the gradients of the tangents at \(A\), \(B\) and \(C\)?
Here are the graphs of another four functions. The equations of these graphs are \[y=f(x)\quad y=f(x+20)-8 \quad y=3f(x-25) \quad \text{and} \quad y=-3f(x)+10.\]
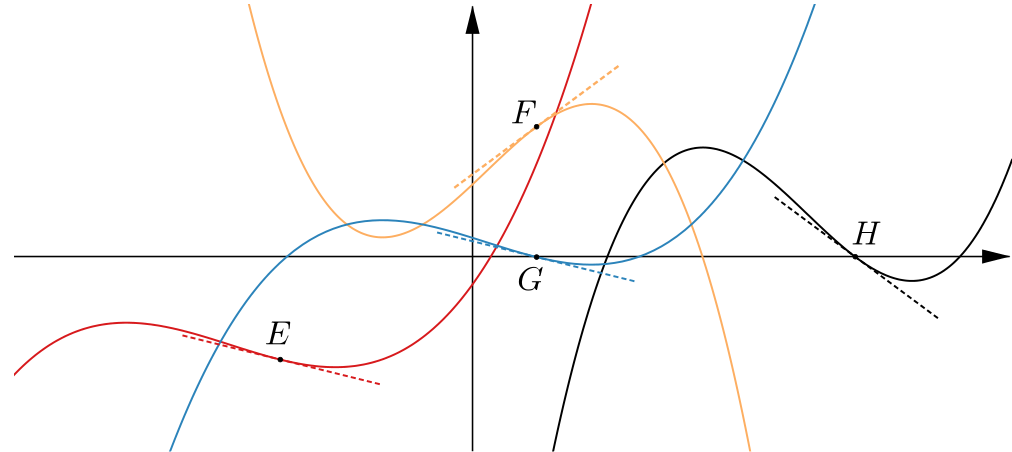
The \(x\)-coordinates of points \(E\), \(F\), \(G\) and \(H\) are \(-15\), \(5\), \(5\) and \(30\) respectively. What can you deduce about these points?
The gradient of the tangent at \(E\) is \(-\tfrac{1}{4}.\) What are the gradients of the tangents at \(F\), \(G\) and \(H\)?

