Transforming things allows us to see them from many points of view. The word transformation is used to describe functions or operations that preserve some structure, so that some characteristics of the input set are preserved in the output set, and some other characteristics are changed in a structured way.
We are familiar with reflecting (which preserves the mirror line), rotating (which preserves the centre-point) and translating in 2-D and 3-D geometry; these all preserve both shape and size. Enlargements preserve shape and proportion, but not usually size, while stretches keep straight lines straight, but change shape and angles. Some of these familiar transformations are explored in Which parabola?. Transformations can also help deepen our understanding of the connections between algebra and geometry; Discriminating offers a good example of this way of thinking.
All circles can be regarded as enlargements and translations of a unit circle; in the standard circle formula \((x-a)^2+(y-b)^2=r^2\) the values of \(a\) and \(b\) give information about the translation and the value of \(r\) gives the enlargement scale factor. You can explore this further with Olympic rings or Teddy bear.
There are other types of geometric transformations. For instance, you may have seen an animation in which a rectangle is ‘pushed over’ to make a parallelogram; or a pile of coins or playing cards pushed over to make a leaning tower. These transformations preserve the base and the height, and the distance each coin is moved is a function of its height. These transformations are called shears. The use of shears in the context of an algebraic problem is explored in It’s a matter of perspective.
Within mathematics, transformations are often used to move an object from a place where it is hard to work with it to a place where it is simpler. For some people moving the object is equivalent to choosing a new way to view the object.
For example it may not always be helpful crunching through a set of simultaneous equations once we know more about parabolas and their equations – this can be seen in Name that graph again.
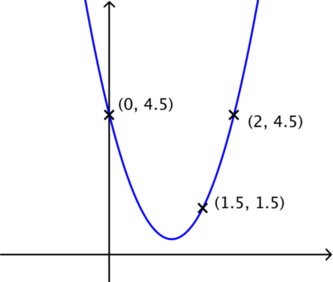
Thinking of functions as transformations of other (possibly more familiar) functions can also be useful. For example, \(y=\sin x\) and \(y=\cos x\) can be regarded as translations of each other, while \(y=\sin^2 x\) can be thought of as a suitable transformation of \(y=\cos x\). Thinking in terms of transforming graphs to move specific features to particular locations can help to solve problems such as Two-way functions, Can you find … cubic edition and Can you find … trigonometry edition.
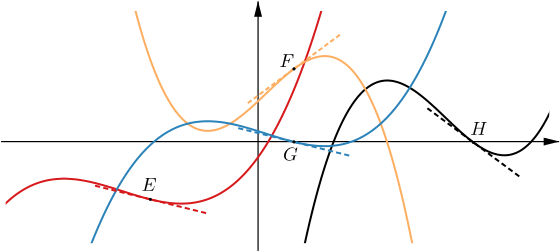
We may also know some information about a function’s graph and the gradient of the tangent lines to the curve or the bounded area below the function, but how does that help understand new functions created by using one of the familiar transformations we saw above? Slippery slopes, Slippery slopes… another derivative and What else do you know? demonstrate how we can use what we know and where some limits of using transformations may lie.
In the opposite direction, one may ask how a function transforms as the parameters in its definition are adjusted. For a circle, changing the parameters in \((x-a)^2+(y-b)^2=r^2\) translates or enlarge it, but for a polynomial such as \(y=ax^2+bx+c\), the impact of changing the coefficients may be less immediately obvious. Resources such as Discriminating, Translating or not? and the “Taking it further” section of the review question Can we solve these simultaneous equations that involve reciprocals? all explore this idea.
So transformations allow us to deepen our understanding of connections between mathematical objects. One result of this is that transforming objects can help us to simplify our calculations and manipulations. It’s important to think about is preserved and what is changed when we transform objects; when performing calculations, this ensures that we can change back after we have done the work.
Transforming is one of the ideas that we have chosen to highlight in our pervasive ideas.

