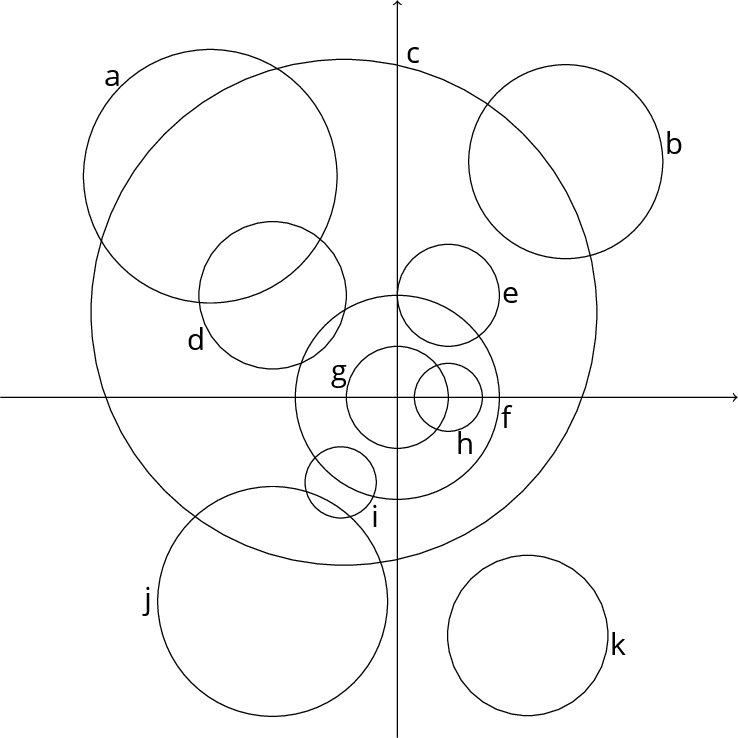
We have thought of 13 circles. 11 of them are drawn accurately on the above graph. Here are the equations of 11 of the original 13 circles.
- \((x+10)^2 +(y+15)^2 = 4\pi^2\)
- \(x^2 + y^2 = 324\)
- \((x+22)^2 + (y+36)^2 = 411\)
- \((x+3\pi)^2 + (y-15)^2 = 1990\)
- \(\bigl(x-21\sqrt{2}\bigr)^2 + \bigl(y-24\sqrt{3}\bigr)^2 = 131\sqrt{5}\)
- \(x^2 + y^2 + 66x - 78y + 2110 = 0\)
- \(x^2 + y^2 = 9\)
- \((x-23)^2 +(y+42)^2 = 200\)
- \(x^2 + y^2 = 81\)
- \((x-18)^2 + (y+36)^2 = 1990\)
- \(x^2 + y^2 - 18x + 45 = 0\)
Can you match them up, find the two missing equations and draw the two missing circles on the graph?

