where \([x]\) indicates the greatest integer less than or equal to \(x\), e.g. \([3] = 3\), \([2.4] = 2\), \([-3.6] = -4\). Sketch the graph of the function for \(-3 \le x \le 3\). What is the range of \(f\)? Is the mapping one-one?
The function \([x]\) defined here is called the floor function.
Note that the value of our function \(f(x)\) will change abruptly at each integer value of \(x\). Let’s look at the behaviour of \(f\) on intervals like \([0,1)\), \([1,2)\), etc.
When \(0 \le x < 1\), we have that \([x] = 0\) and so \[\begin{equation*} f(x) = \left| x + [x] \right| = |x| = x. \end{equation*}\] When \(1 \le x < 2\), we have \([x] = 1\) so \[\begin{equation*} f(x) = \left| x + [x] \right| = |x+1| = x + 1 \end{equation*}\] and similarly for all other intervals of the form \([n,n+1)\) where \(n\) is a positive integer, \[\begin{equation*} f(x) = x + n . \end{equation*}\] On the other hand, when \(-1 \le x < 0\), we have \([x] = -1\) and so \[\begin{equation*} f(x) = \left| x + [x] \right| = |x-1| = -x + 1. \end{equation*}\] Similarly, for all intervals of the form \([n,n+1)\) with \(n < 0\), \[\begin{equation*} f(x) = -x - n . \end{equation*}\]These considerations lead to the following graph.
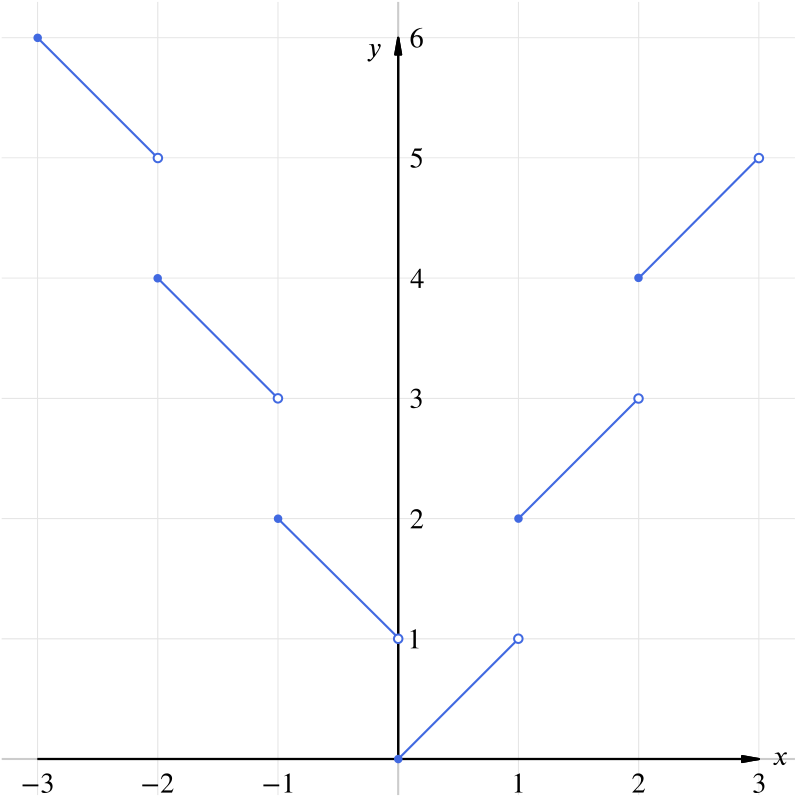
As can be seen from the graph, the range of \(f\) is \[f(x)\geq 0, f(x)\neq 1,3,5,\ldots.\]
Notice that \(f(-1)=f(1)=2\) and similarly for other non-zero integer values of \(x\). Hence the mapping is not one-to-one.
The function \(g\) is defined by \(g \colon x \to \left| x + [x] \right|\), \(x \in \mathbb{R}_+\), \(x \notin \mathbb{Z}_+\). Find the rule and domain of the inverse function \(g^{-1}\).
The notation \(x \in \mathbb{R}_+\), \(x \notin \mathbb{Z}_+\) means that the domain of \(g\) is the real numbers greater than zero but excluding all the positive integers. Where the question asks for the ‘rule’ it means an algebraic definition of the function.
Remember that an inverse function does not exist for a function such as \(f\) that is not one-to-one. The restricted domain of \(g\) means that it is one-to-one and does have an inverse.
Notice also that with the restricted domain, \(x+[x]\) is always positive, so the definition of \(g\) can (more conveniently) be written without the modulus sign.
By definition, the domain of \(g^{-1}\) is the same as the range of \(g\). From the graph, we can see that this is \[0<x<1\text{ and }2<x<3\text{ and }\ldots\text{ and }2n<x<2n+1\ldots\] where \(n\) is a positive integer. This can be written as \[(0,1) \cup (2,3) \cup (4,5) \ldots \cup (2n,2n+1) \cup \ldots .\]
To find the rule that defines \(g^{-1}\), let’s first think about what \(g\) is doing. We can consider the number \(x\) as being made up of two parts – the whole number part \([x]\) and its fractional part which we call \(a\) (such that \(0<a<1\)). Then \[x=[x]+a\] and \[g(x)=x+[x] = 2[x]+a.\] In other words, the function \(g\) doubles the whole number part and keeps the fractional part the same. We can think about \(g\) as a function machine.
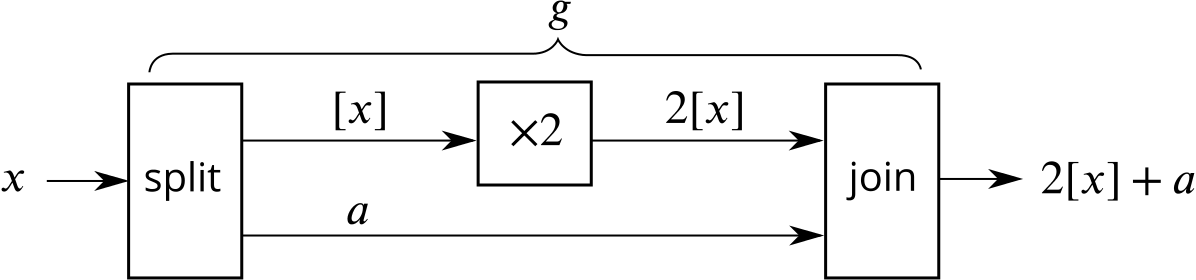
We have defined the operation ‘split’ to mean turn \(x\) into a whole number and a fractional part between \(0\) and \(1\). The operation ‘join’ is its inverse which is actually just addition.
Now we can draw the inverse function machine.
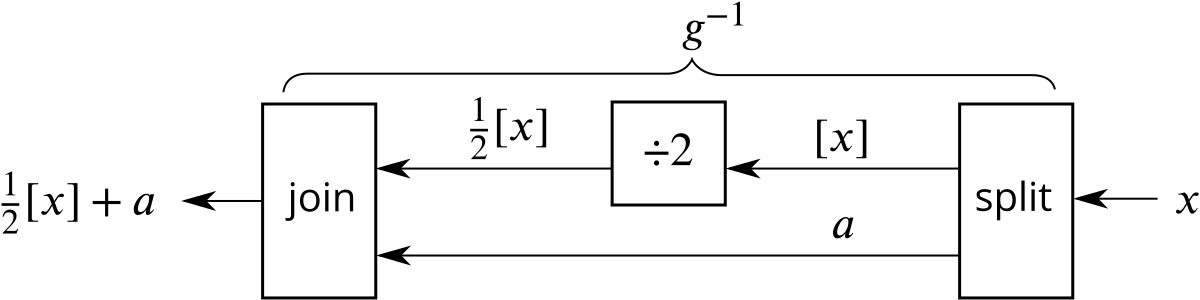
So now we see that \[g^{-1}(x)=\frac{1}{2}[x]+a = \frac{1}{2}[x]+x-[x] = x-\frac{1}{2}[x].\]
Alternatively, we are to find the function \(g^{-1}\) such that \(g^{-1}(x + [x]) = x\) whenever \(x\) is in the domain of \(g\). So we want to write \(x\) as a function of \((x+[x])\).
We note that \([x + [x]] = 2[x]\), so we can write \[\begin{equation*} x = x + [x] - [x] = (x + [x]) - \frac{[x + [x]]}{2}. \end{equation*}\]Thus, the required rule is \(g^{-1}(x) = x - \dfrac{[x]}{2}\), as before.
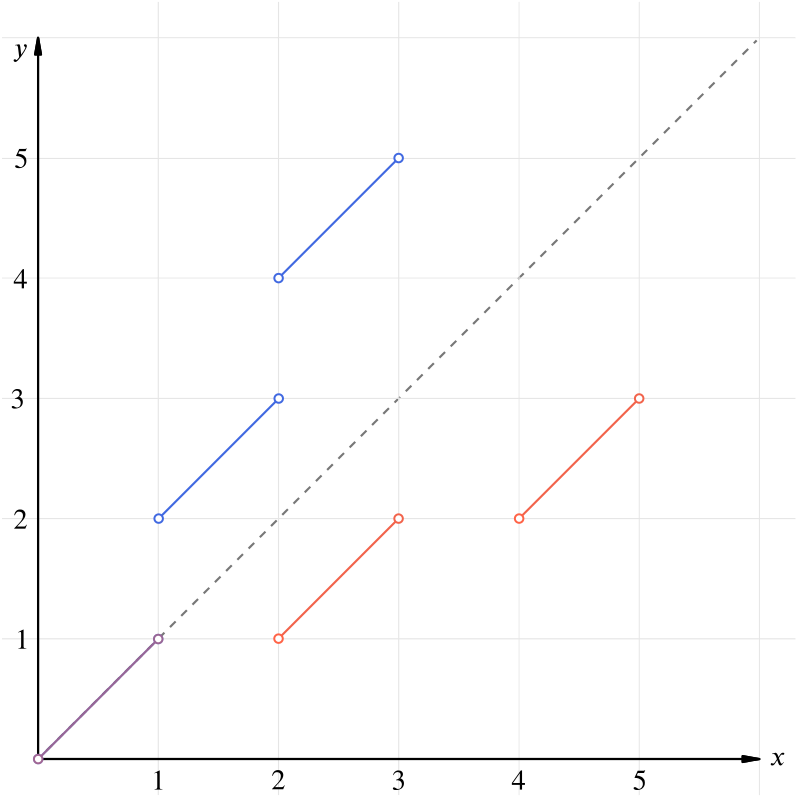
The graph of \(y = g(x)\) is in blue, the line \(y = x\) is a dashed line, and \(y=g^{-1}(x)\) is in red.
We can reply by pointing out that \(5.75\) does not lie in the domain of \(g^{-1}\), even though the rule that defines \(g^{-1}\) can be applied, in principle, to any real number.

