- The functions \(f\) and \(g\) are defined by \[\begin{align*} f&: x\mapsto e^x, &&x\in\mathbb{R}, \\ g&: x\mapsto x-1, &&x\in\mathbb{R}. \end{align*}\] Sketch in a single diagram the graphs of \(f\) and the composite functions \(gf\) and \(fg\), labelling each graph clearly.
First, we’ll find the composite functions \(gf\) and \(fg\). We have \[gf = e^x-1\] and \[fg = e^{x-1}.\]
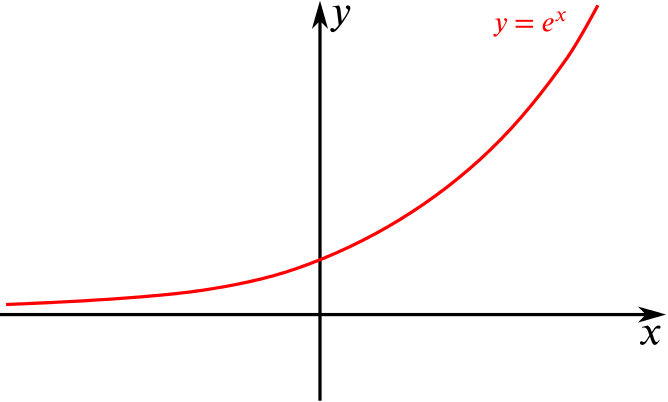
Let’s first sketch \(y=e^x\). We know that \(e^x\to 0\) as \(x\to -\infty\), the graph crosses the \(y\)-axis at \((1,0)\) and it is strictly increasing. So it looks roughly like this:
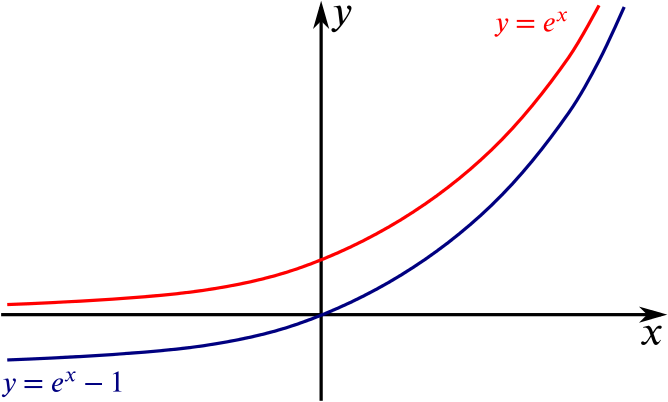
Now let’s add a sketch of \(e^x-1\). We know that this is a translation of \(y=e^x\) by \(-1\) in the \(y\)-direction, and that \(y=e^x\) and \(y=e^x-1\) cannot intersect. So our graph now looks like:
Finally, we add \(y=e^{x-1}\). This is a translation of \(y=e^x\) by \(1\) in the \(x\)-direction. The graphs of \(y = e^x\) and \(y=e^{x-1}\) don’t meet, but \(y=e^{x-1}\) does meet \(y=e^x-1\). So a sketch of the three functions looks like this:
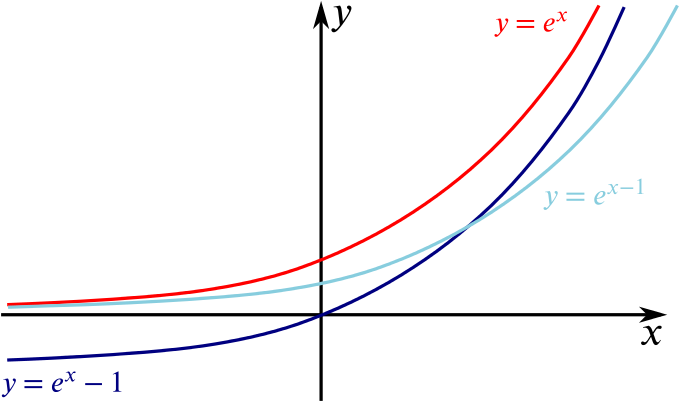
State briefly the relationship
- between the graphs of \(f\) and \(gf\),
The graph of \(gf\) is a translation of \(f\) by one unit in the negative \(y\) direction.
- between the graphs of \(f\) and \(fg\).
The graph of \(fg\) is a translation of \(f\) by one unit in the positive \(x\) direction.
- Express \((1-x)(x-3)\) in the form \(a-(x-b)^2\), where \(a\) and \(b\) are constants.
We expand \((1-x)(x-3)\) to obtain \(-x^2+4x-3\).
Completing the square, we find that \((1-x)(x-3)=-x^2+4x-3=-(x-2)^2+4-3=1-(x-2)^2.\)
We could also do this by expanding both expressions and solving for \(a\) and \(b\) after comparing coefficients.
State the coordinates of the maximum point on the graph of \(y=(1-x)(x-3)\), and state what symmetry the graph possesses.
From the rewriting of the equation \(y=(1-x)(x-3)\) in the form \(y=1-(x-2)^2\), we see that the maximum point on the graph occurs when \(y=1\) because the expression \(-(x-2)^2\) must be negative or zero. The expression \(-(x-2)^2\) is \(0\) when \(x=2\) so the maximum point has coordinates \((2,1)\). The graph possesses line symmetry about \(x=2\).
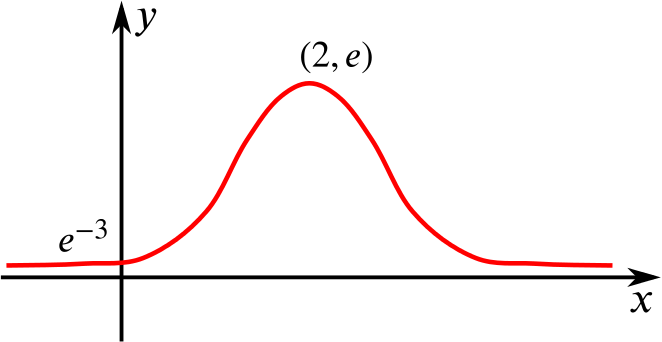
Sketch the graph of \(y=e^{(1-x)(x-3)}\).
So the graph
has a maximum at \(x=2\), \(y=e\);
has symmetry about \(x=2\);
has its \(y\)-intercept at \(e^{-3}\);
sees \(y\rightarrow0\) as \(x\rightarrow\pm\infty\).
The sketch is