A function is defined by \(f:x\mapsto \dfrac{1}{3-2x}\) for all values of \(x\) except \(x=\dfrac{3}{2}\).
- Find the values of \(x\) which map on to themselves under the function \(f\).
We seek \(x\) such that \(f(x)=x\), so we need to solve \[ x=\frac{1}{3-2x}. \] Multiplying both sides by \(3-2x\), we find that \[ 3x-2x^2=1, \] so we must solve the quadratic equation \[ 2x^2-3x+1=0. \] By inspection, we see that \[ 2x^2-3x+1=(2x-1)(x-1), \] therefore the points which are mapped to themselves by \(f\) are \(x=\dfrac{1}{2}\) and \(x=1\).
A function is defined by \(f:x\mapsto \dfrac{1}{3-2x}\) for all values of \(x\) except \(x=\dfrac{3}{2}\).
- Find an expression for \(f^{-1}\).
A function is defined by \(f:x\mapsto \dfrac{1}{3-2x}\) for all values of \(x\) except \(x=\dfrac{3}{2}\).
- Evaluate \(ff(2)\).
We have that \(f(2)=\dfrac{1}{3-4}=-1\), so \(ff(2)=f(-1)=\dfrac{1}{3+2}=\dfrac{1}{5}\).
- Sketch the graph of \(y=|x^2-4x+3|\) for the domain \(0\le x \le 5\), and state the corresponding range of \(y\).
To start with, let’s consider \(x^2-4x+3=(x-1)(x-3)\). Using our knowledge of quadratics, we can sketch this straightforwardly.
When \(x=0\), \(x^2-4x+3=3\), and when \(x=5\), \(x^2-4x+3=8\). The minimum occurs at the midpoint of the two roots, when \(x=2\), and here \(x^2-4x+3=-1\).
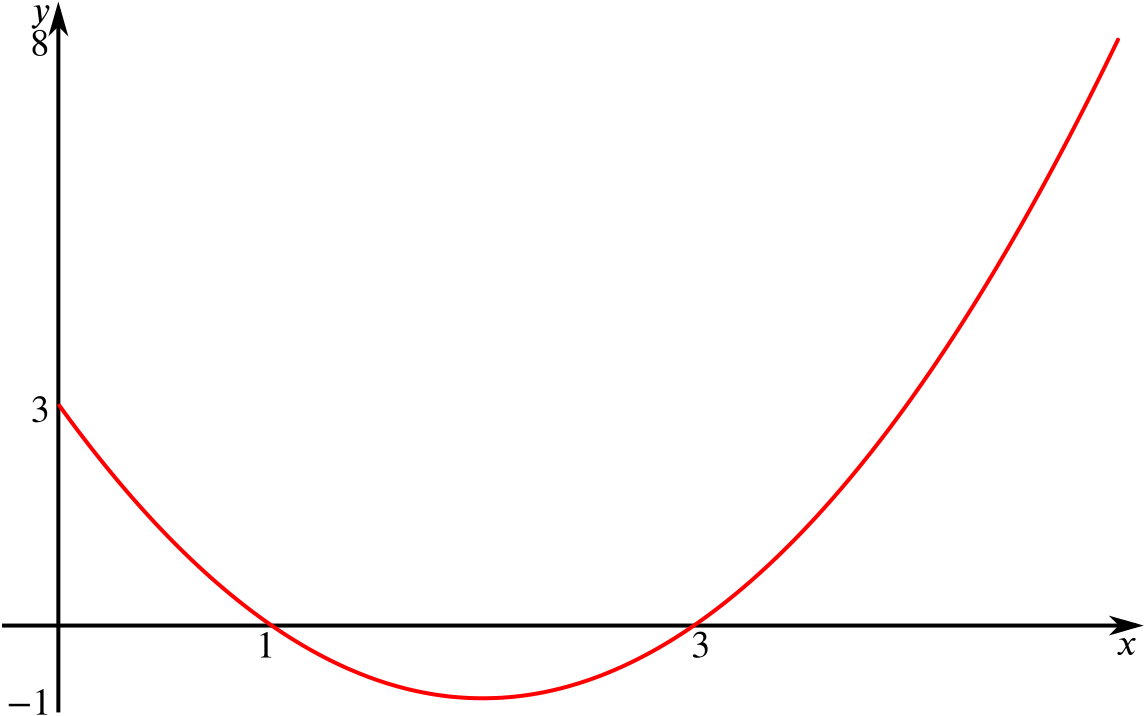
To make this into a sketch of \(y=|x^2-4x+3|\), we must reflect the part where \(x^2-4x+3<0\) in the \(x\)-axis.
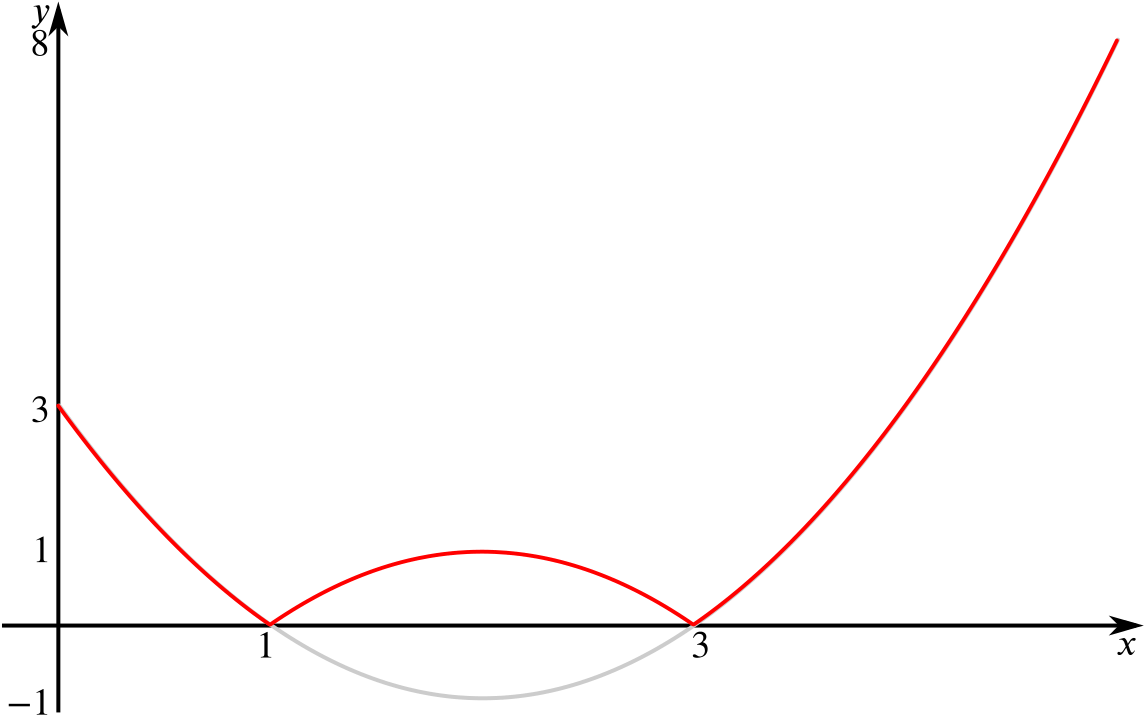
The largest value of \(y\) is \(8\) when \(x=5\). Therefore for the domain \(0\le x\le 5\), we have that the range of \(y=|x^2-4x+3|\) is \(0\le y\le 8\).

