Find the ranges of \(f\) and \(g\), and sketch the graph of \(g\).
The function \([x]\) defined here is known as the floor function.
From the definition of the floor function, the output value of \(f\) will always be an integer. Since the input \(x\) can be any real number the range of \(f\) is all the integers, \(\mathbb{Z}\).
The function \(g(x)=x-[x]\) which means it subtracts the whole number part, leaving only the fractional part of the input value \(x\).
For integer values of \(x\), \([x]=x\) which means that \(g(x)=0\). So the graph of the function looks like this.
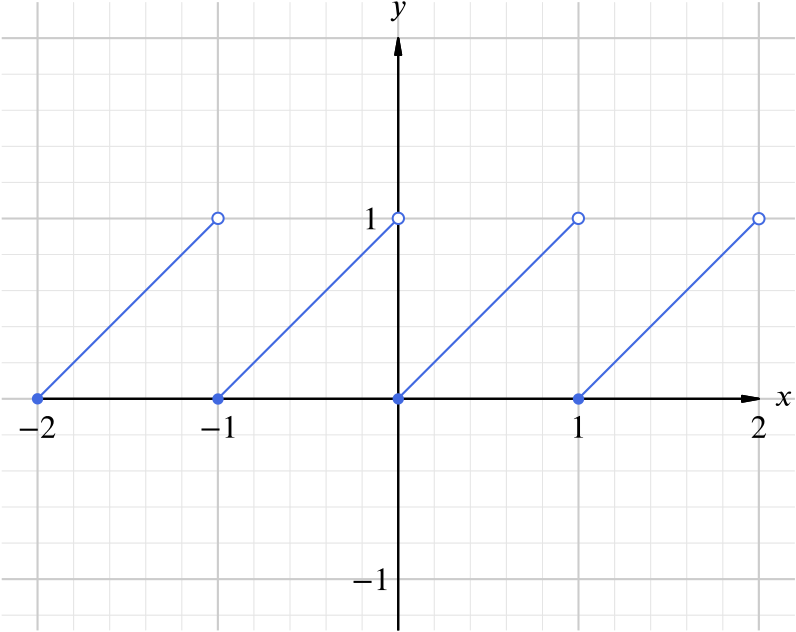
The range is \(0\leq g(x)<1\).
Determine the solution sets of the equations
- \(f(x) = g(x)\)
The left-hand side is always an integer, while the only integer value that the right-hand side can take is zero, which occurs whenever \(x\) is an integer.
The solution set is therefore \(x=0\).
- \(fg(x) = g\,f(x)\)
The equation is therefore satisfied regardless of the value of \(x\). The solution set is the real numbers, \(\mathbb{R}\).

