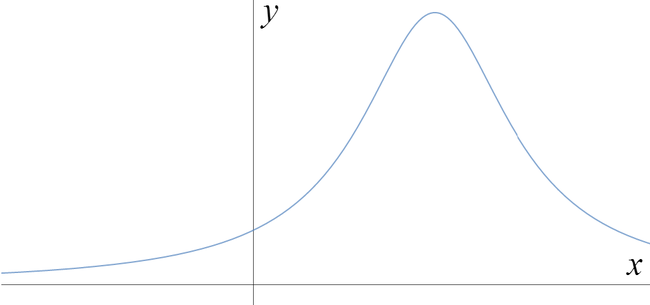
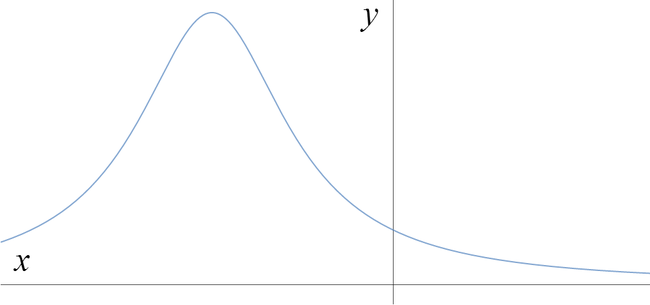
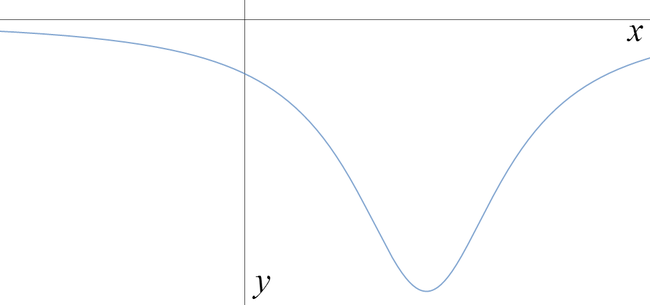
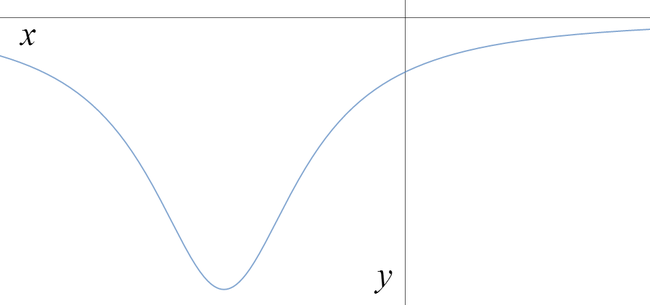
Which of the graphs below is a sketch of \[y = \frac{1}{4x-x^2-5}\; ?\]
|
|
|
|
|
|
We can complete the square. We have \(4x-x^2-5 = -(x^2-4x) -5 = -((x-2)^2-4)-5 = -(x-2)^2+4-5 = -(x-2)^2-1\).
So the graph is \[y = \frac{1}{-(x-2)^2-1},\] which shows the function is always negative, and has a minimum value of \(y=-1\) at \(x=2\).
Hence the correct graph is c.