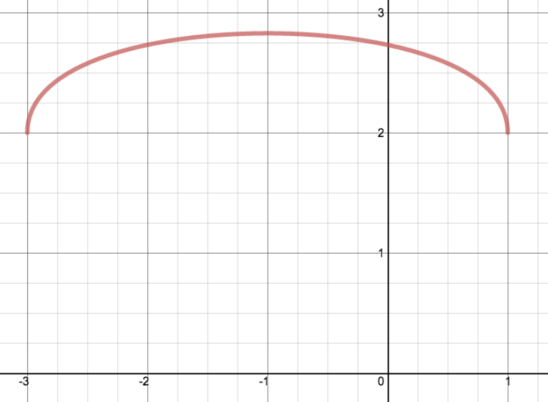
- Sketch the curve \(y = \sqrt{1 - x} + \sqrt{3 + x}\). Use your sketch to show that only one real value of \(x\) satisfies \[\sqrt{1 - x} + \sqrt{3 + x} = x + 1,\] and give this value.
First, we identify some key properties of the graph \(y = \sqrt{1 - x} + \sqrt{3 + x}\) so we can sketch it.
The right-hand side is defined only for \(-3 \leq x \leq 1\), so the endpoints are at \((-3,2)\) and \((1,2)\).
- If we evaluate the function (let’s call it \(f\)) at a few points, we find that
\[\begin{align*}
f(-3) &= 2, \\
f(-2) &= 1 + \sqrt{3}, \\
f(-1) &= 2\sqrt{2}, \\
f(0) &= 1 + \sqrt{3}, \\
f(1) &= 2.
\end{align*}\]
This suggests that the function is symmetrical about the line \(x = -1\). In fact, we can show this, since \[\sqrt{1 - x} + \sqrt{3 + x} = \sqrt{2 - (x+1)} + \sqrt{2 + (x+1)}.\] So our curve is the graph of \(y = g(x) = \sqrt{2 - x} + \sqrt{2 + x}\) shifted \(1\) to the left, and it’s easy to see that the graph of \(y = g(x)\) is symmetrical about the \(y\)-axis.
- Although this is not essential to sketch the curve, we can differentiate to find the stationary points. We have \[\frac{dy}{dx} = \frac{-1}{2\sqrt{1 - x}} + \frac{1}{2\sqrt{3 + x}}\] so to find the stationary points we find when this is zero. We have \[\sqrt{1 - x} = \sqrt{3 + x}\] \[\Longrightarrow 1 - x = 3 + x\] \[\Longrightarrow x = -1,\] and we can check that \(x = -1\) really does give derivative \(0\).
Clearly this is a maximum because the other points evaluated have values smaller than \(2\sqrt{2}\).
- We can also see that the gradient at the endpoints must be infinite, because when the expression for the derivative is evaluated at either of them, one of the fractions will be of the form \(\frac{1}{0}\).
This gives us enough information to sketch the curve.
Now to solve the equation given, we also plot the graph of \(y = x + 1\) and find where they intersect.
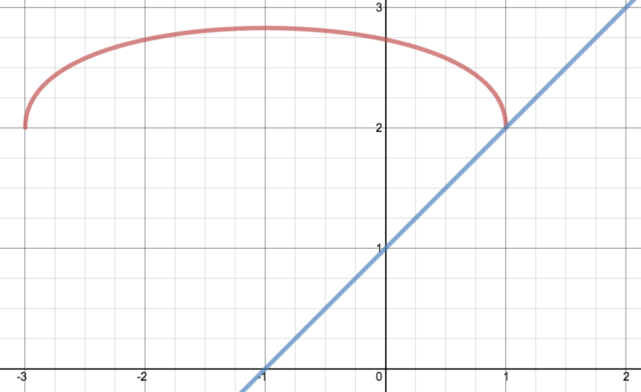
So we clearly see that \(x = 1\) is the only (real) solution.
- Determine graphically the number of real values of \(x\) that satisfy \[2\sqrt{1 - x} = \sqrt{3 + x} + \sqrt{3 - x}.\] Solve this equation.
Here we use a similar method, and sketch the graphs of the curves \(y = \sqrt{3 + x} + \sqrt{3 - x}\) and \(y = 2\sqrt{1 - x}\).
The first is essentially the same curve as in (i), but defined on the interval \(-3 \leq x \leq 3\), with its maximum at \((0,2\sqrt{3})\) and symmetry about the \(y\)-axis.
The second curve is similar to the graph of \(\sqrt{x}\), with a translation, reflection and enlargement applied to it:
Translation of one unit to the left: \(x \mapsto 1 + x\)
Reflection in the \(y\)-axis: \(x \mapsto - x\)
Enlargement by a scale factor of 2: \(f(x) \mapsto 2f(x)\)
We can also see that the graph passes through \((1,0)\) and \((0,2)\).
From this, we sketch the two graphs on the same axes.
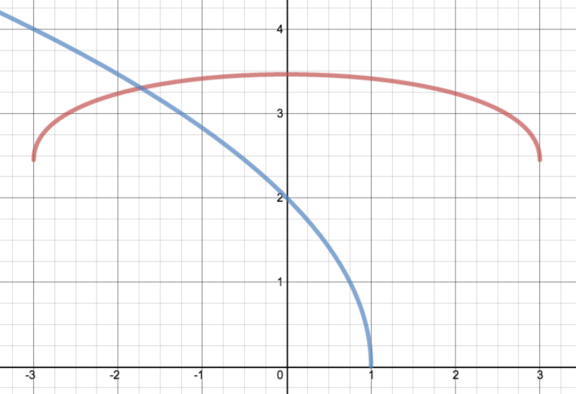
These curves intersect only once, when \(x < 0\).
We use algebra to solve the equation: \[\begin{align*} 2\sqrt{1 - x} &= \sqrt{3 + x} + \sqrt{3 - x} \\ \Longrightarrow 4(1 - x) &= 3 + x + 2\sqrt{3 + x}\sqrt{3 - x} + 3 - x \\ \iff 4 - 4x &= 6 + 2\sqrt{(3 + x)(3 - x)} \\ \iff 1 + 2x &= -\sqrt{9 - x^2} \\ \Longrightarrow 1 + 4x + 4x^2 &= 9 - x^2 \\ \iff 5x^2 + 4x - 8 &= 0. \end{align*}\] We can solve this quadratic equation, to find that \[\begin{align*} x &= \frac{-4 \pm \sqrt{16 + 4\times5\times8}}{10} \\ &= \frac{-4 \pm \sqrt{16\times11}}{10} \\ &= \frac{-4 \pm 4\sqrt{11}}{10} \\ &= \frac{-2}{5}(1 \pm \sqrt{11}). \end{align*}\]Then one of these roots is positive and one is negative. However, only the negative root is a valid solution, as the sketch shows. So the solution of this equation is \[x = \frac{-2}{5}(1 + \sqrt{11}).\]

