The graph of \(y=\sin^2{\sqrt{x}}\) is drawn in
|
|
|
|
|
|
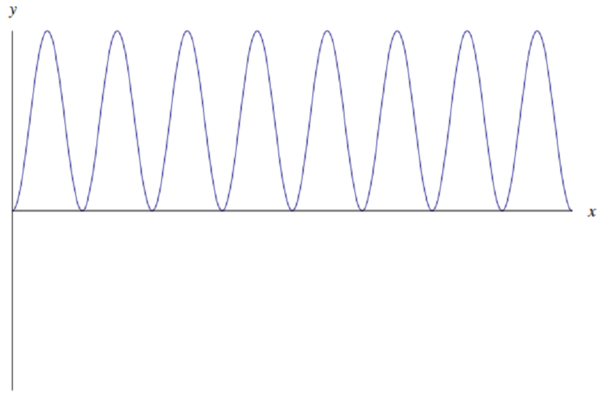
The function \(y=\sin^2{\sqrt{x}}\) is positive for any positive \(x\), so it cannot be (a).
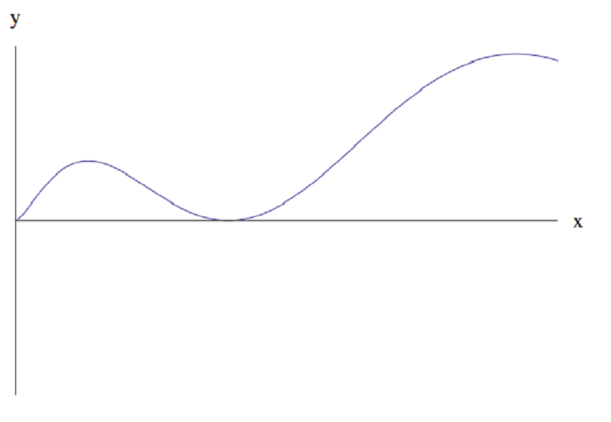
The local maximum of \(y=\sin^2{\sqrt{x}}\) is \(1\) for \(\sqrt{x} = \left(\dfrac{\pi}{2}\right), \left(\dfrac{3\pi}{2}\right), \left(\dfrac{5\pi}{2}\right) ...\), so it cannot be (c) as its first two local maxima are of different values.
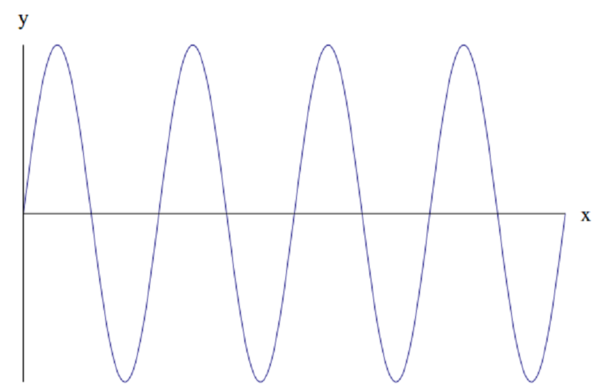
And the frequency of our function is not constant, as it is in the case of \(\sin x\). We can see this by looking at the \(x\) values of the first few maxima: \[x = \dfrac{\pi^2}{4}, \dfrac{9\pi^2}{4}, \dfrac{25\pi^2}{4}...\]
These are not equally separated, so it cannot be (d).
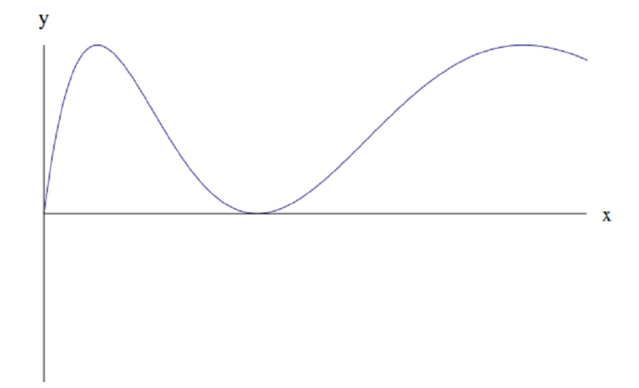
Which means the correct answer is (b).