State the ranges of \(f\) and \(g\), and show that if \(h\) denotes the composite function \(f \circ g\), then \[h(x)+f(x)=0.\]
The range of \(f\) is \(\mathbb{R}\) and the range of \(g\) is \(\mathbb{R}_+\).
It is often helpful for domain and range questions to think about the graph of the relevant functions; here is the graph of \(y=f(x)\):
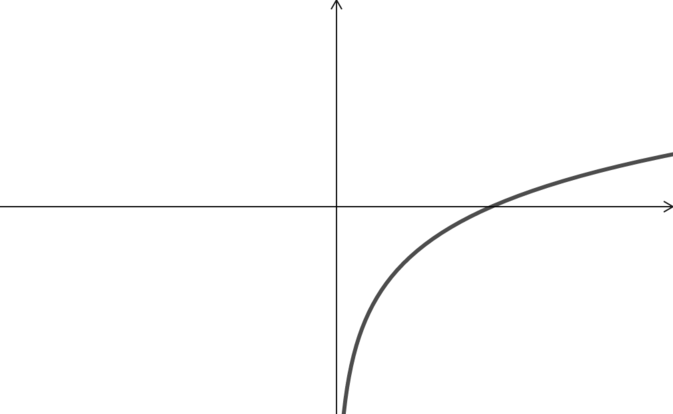
We can see that the graph gives every \(y\) value for some \(x\) value, so the range is the whole of \(\mathbb{R}\).
Here is the graph of \(y=g(x)\) (confining the domain to only \(\mathbb{R}_+\)):
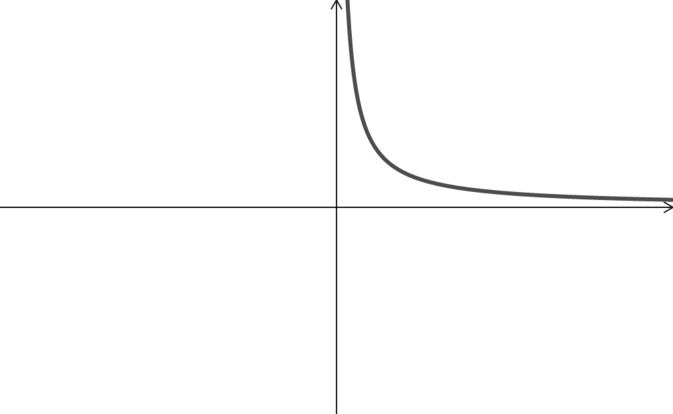
Then it’s clear that the values of \(y\) which the graph passes through are those greater than zero, so the range of \(g\) is \(\mathbb{R}_+\).
So \(h(x)+f(x)=-\log_a x+\log_a x=0\).
Explain briefly why the composite function \(g \circ f\) cannot be properly defined unless the domain is restricted to a subset of \(\mathbb{R}_+\), and state a possible subset which would be suitable.
For the composition \(f_2 \circ f_1\) of two functions, \(f_1\) and \(f_2\), to be properly defined, we must have the range of \(f_1\) contained within the domain of \(f_2\). (Otherwise, for some \(x\) in the domain of \(f_1\), we would have \(f_1(x)\) not in the domain of \(f_2\), so \(f_2(f_1(x))\) will not be defined.)
In this case, we are considering \(g\circ f\) so \(f_2=g\) and \(f_1=f\). Therefore we require the range of \(f\) to be contained within the domain of \(g\).
But the domain of \(g\) is \(\mathbb{R}_+\) while the range of \(f\) is \(\mathbb{R}\). So the range of \(f\) is not contained within the domain of \(g\), thus \(g \circ f\) is not properly defined unless we restrict the domain to a subset of \(\mathbb{R}_+\).
For a suitable subset, we need the range of \(f\) with this restricted domain to be a subset of \(\mathbb{R}_+\). We see that \(f(x)>0\) when \(x>1\), so any subset of \(\{x:x>1\}\) (the real numbers greater than \(1\)) would suffice.
Define fully the inverses of \(f\) and \(g\), and determine whether or not \(h^{-1}(x)+f^{-1}(x)=0\).
When defining a function, it is vital to specify the domain.
Recall that for any function \(f\), the domain of \(f^{-1}\) is the range of \(f\): every possible output of \(f\) has to be an allowable input to \(f^{-1}\) to get back to the original value.
As \(f(x)=\log_a x\), to find the inverse, we can write \(x=f(y)\) and rearrange to find \(y\) in terms of \(x\).
What we’re really doing is saying that \(f\bigl(f^{-1}(x)\bigr)=x\) and then writing \(y=f^{-1}(x)\). So we are using the result that \(f\circ f^{-1}\) and \(f^{-1}\circ f\) are both the identity function.
So \(f^{-1}(x)=a^x\) for \(x\) in \(\mathbb{R}\).
For \(g(x)\), we have \[\begin{align*} &&x&=g(y)&&\quad\\ \implies&&x&=\frac{1}{y}\\ \implies&&y&=\frac{1}{x} \end{align*}\]So \(g^{-1}(x)=1/x\) for \(x\) in \(\mathbb{R}_+\).
For the final part, we start by finding \(h(x)\): \[\begin{align*} &&x&=h(y)&&\quad\\ \implies&&x&=-\log_a y\\ \implies&&-x&=\log_a y\\ \implies&&a^{-x}&=y \end{align*}\]so \(h^{-1}(x)=a^{-x}\).
Thus \(h^{-1}(x)+f^{-1}(x)=a^{-x}+a^x>0\) for all \(x\), so \(h^{-1}(x)+f^{-1}(x)\ne 0\).

