State the range of the function and sketch the graph of \(y=f(x)\).
We know that the graph \(y=-5-x\) is a straight line on the given interval, running from (-3, -2) down to \((-1,-4)\). Note that \((-1,-4)\) is included in the graph, but \((-3,-2)\) is not.
Similarly, we know that the graph \(y=5-x\) is a straight line on the given interval, running from \((1,4)\) down to \((3,2)\). Note that neither \((1,4)\) nor \((3,2)\) is included in the graph.
We should know the graph of \(y = x^3\), and \(y = 2x^3\) is a stretch of this by a scale factor of \(2\) in the \(y\)-direction. Its starting point on the given interval is \((-1,-2)\), and its endpoint is \((1,2)\). Note that \((1,2)\) is included in the graph, but \((-1,-2)\) is not.
The graph of \(y=f(x)\) is
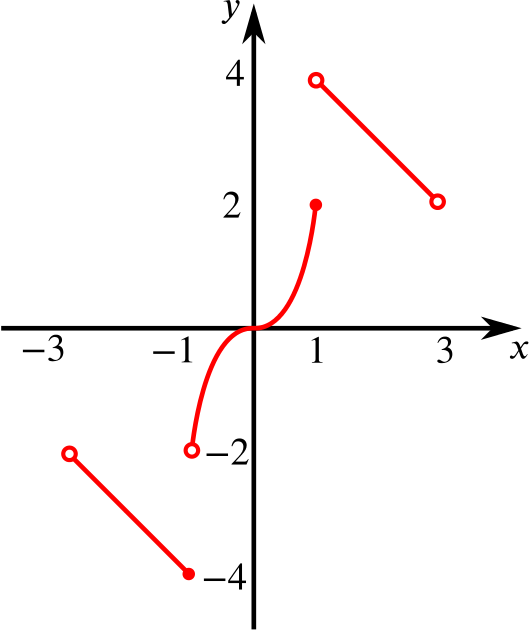
The solid endpoints are included in the graph, while the empty endpoints are not. Therefore the range of \(f\) is \(\{y:-4\le y<4, y\ne -2\}\).
Define the inverse relation in similar form and determine whether this inverse relation is a function.
Then \(g\) IS a function because, as we can see from our sketch, the function \(f\) is \(1-1\). The evidence for this is that no horizontal line cuts our graph of \(y = f(x)\) in two places.
We say the original function \(f\) is injective; no point is mapped to two different points by \(g\), the inverse.

