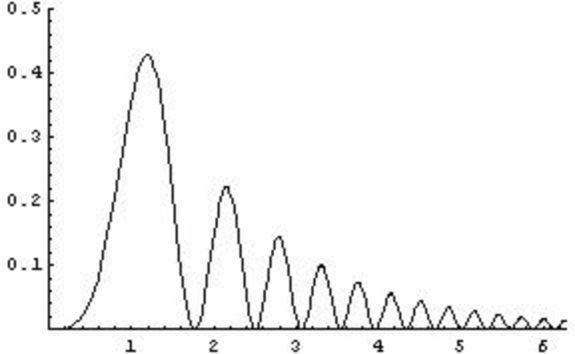
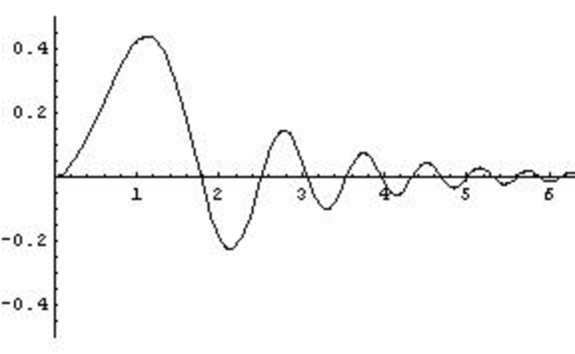
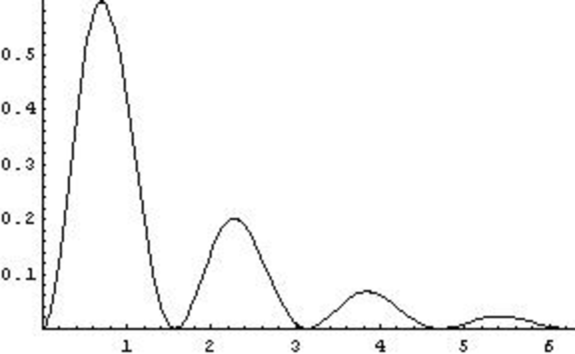
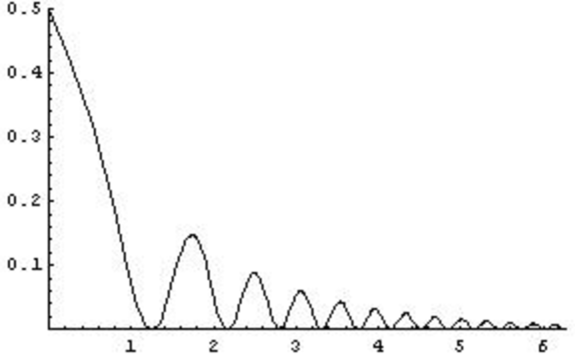
On which of the axes below is a sketch of the graph \[y = 2^{-x} \sin^2 (x^2)?\]
|
|
|
|
|
|
Both \(2^{-x}\) and \(\sin^2(x^2)\) are functions that are never negative, so \(y\geq0\), which discounts b.
At \(x=0\), \(2^{-x} = 1\) and \(\sin^2 (x^2)=0\), so \(y(0)=0\), which discounts d.
Finally, the graph meets the \(x\)-axis when \(\sin^2 (x^2) = 0\), which occurs when \(\sin (x^2)=0\), so at
\[x = \sqrt{\pi}, \sqrt{2\pi}, \sqrt{3\pi}, \ldots.\]
These are not evenly spaced as in c. These values get closer together as \(x\) increases, as in a.
Hence the answer is (a).