In an examination, candidates could take any one, any two or all of Latin, French and German.
Out of \(100\) candidates \(4\) took Latin only, \(13\) took French only and \(12\) took German only. There were \(5\) who took all three languages and \(20\) who did not take French.
The average mark in French of all of the candidates who took this subject was \(50\)%. Within this group there were the following average marks in French:
\(\qquad\) Those taking French only, \(57\)%.
\(\qquad\) Those taking French and Latin, \(45\)%.
\(\qquad\) Those taking French and German, \(52\)%.
\(\qquad\) Those taking all three languages, \(35\)%.
Calculate the number who took Latin and German, the number who took French and Latin and the number who took French and German.
Let’s summarise with a Venn diagram.
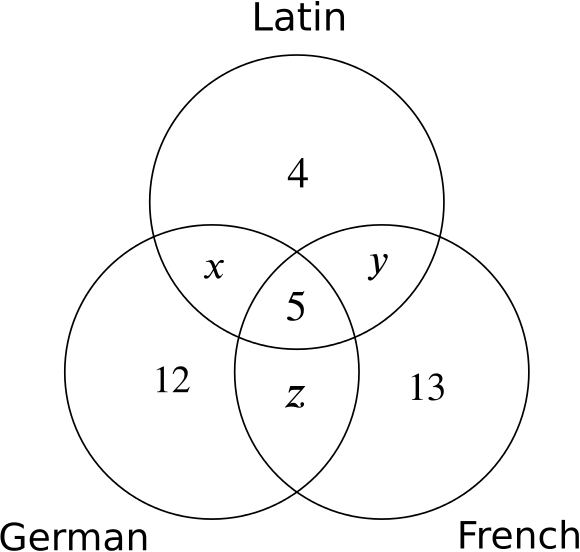
Note that the question doesn’t allow for someone not taking any of the three languages. Everyone here takes at least one language.
The question tells us that \(20\) candidates didn’t take French. Therefore 20 candidates took only Latin, only German, or Latin and German.
From our diagram, we see that this means \[4+12+x=20,\] and so \(x=4\).
Let’s use that the total number of candidates is \(100\). We find that \[4+13+12+4+y+z+5=100,\] which means that\[\begin{equation}\label{eq:eqn1} y+z=62. \end{equation}\]
What about the averages? We have that \(80\) candidates took French, and their average mark was \(50\), so the total number of marks earned was \(4000\).
Note now that when the question says ‘French and German’ it means ‘French and German but not Latin’.
Since the average mark of those taking only French was \(57\), and \(13\) candidates only took French, this accounts for \(57\times 13=741\) marks.
The total marks earned by those taking French and Latin is \(45y\).
The total number of marks earned by those taking French and German is \(52z\).
Finally, the number of marks earned by those taking all three languages is \(35\times 5=175\).
This tells us that \[4000=741+45y+52z+175.\]
Rearranging \(\eqref{eq:eqn1}\), we find that \(z=62-y\), and on substituting this in, we have \[4000=741+45y+52(62-y)+175,\] which yields \[7y=140,\] and so \(y\) is \(20\), and \(z\) is \(62-20=42\).
Our completed Venn diagram looks like this:
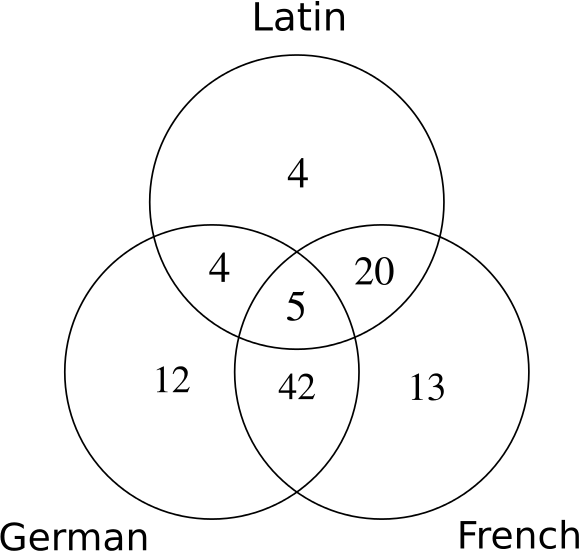
So the number who took Latin and German is \(4\), the number who took French and Latin is \(20\), and the number who took French and German is \(42\).

