In the questions below, the people involved make statements about each other. Each person is either a saint (S) who always tells the truth or a liar (L) who always lies.
Six people, \(P_1, P_2,\dots,P_6\) sit in order around a circular table with \(P_1\) sitting to \(P_6\)’s right, as shown in the diagram below.
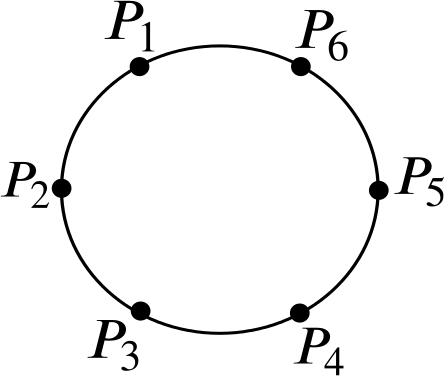
Suppose all six people say “the person directly opposite me is telling the truth”. One possibility is that all six are lying. But, in total, how many different possibilities are there? Explain your reasoning.
Suppose now that all six people say “the person to my left is lying”. In how many different ways can this happen? Explain your reasoning.
Now \(n\) people \(Q_1\), \(Q_2\), …, \(Q_n\) sit in order around a circular table with \(Q_1\) sitting to \(Q_n\)’s right.
Suppose that all \(n\) people make the statement “the person on my left is lying and the person on my right is telling the truth”. Explain why everyone is lying.
Suppose now that every person makes the statement “either the people to my left and right are both lying or both are telling the truth”. If at least one person is lying, show that \(n\) is a multiple of three.

