In a certain school there are \(127\) boys in one particular year. They may study one or more (or none) of the languages Latin, French, and German. No boys study both Latin and German; \(18\) study both French and German, half as many French and Latin; \(21\) study Latin only; \(70\) study a language but not German; \(82\) study one or more of the two modern languages. By using Venn diagrams, or otherwise, find how many boys study each language and how many study none.
Let us start with writing all numbers into a Venn diagram which we get immediately from the question.
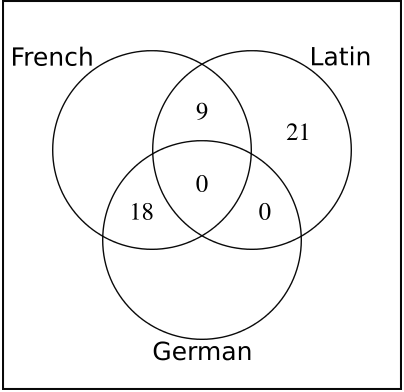
Now we also know that \(70\) study a language but not German, which means that \(40\) study French alone.
Now if \(82\) study one or more of the two modern languages, \(15\) must study German alone.
Adding up, that leaves \(24\) out of \(127\) studying no languages at all.
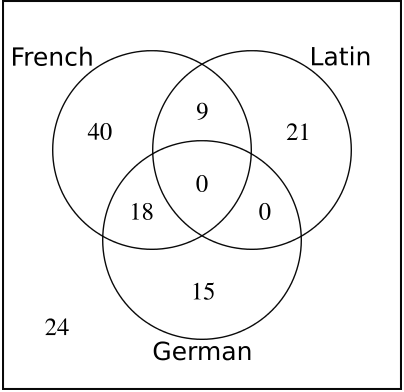
Thus \(67\) study French, \(33\) study German, \(30\) study Latin, and \(24\) study no languages at all.

