Amy and Brian play a game together, as follows. They take it in turns to write down a number from the set \(\{ 0,1,2 \}\), with Amy playing first. On each turn (except Amy’s first turn), the player must not repeat the number just played by the previous player.
In their first version of the game, Brian wins if, after he plays, the sum of all the numbers played so far is a multiple of \(3\). For example, Brian will win after the sequence \[(2,0)\; (1,2)\; (1,0)\] (where we draw a bracket around each round) because the sum of the numbers is \(6\). Amy wins if Brian has not won within five rounds; for example, Amy wins after the sequence \[(2,0)\; (1,2)\; (1,2)\; (0,2)\; (1,2)\]
- Show that if Amy starts by playing either \(1\) or \(2\), then Brian can immediately win.
If Amy plays \(1\), Brian can play \(2\) and win; similarly if Amy plays \(2\), Brian can play \(1\) and win.
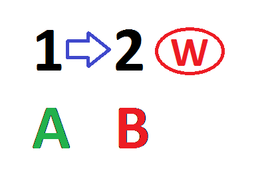
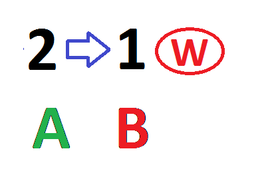
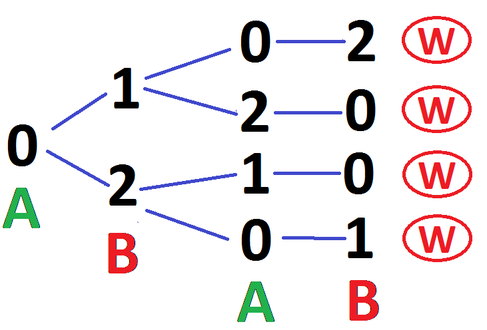
- Suppose, instead, Amy starts by playing \(0\). Show that Brian can always win within two rounds.
If Amy starts with \(0\), Brian can play \(1\).
Then Amy can play \(0\) or \(2\). If she plays \(0\), Brian plays \(2\) and wins; if she plays \(2\), Brian plays \(0\) and wins.
If Amy starts with \(0\), and Brian plays \(2\), then Amy can play \(1\), in which case Brian plays \(0\) and wins; if she plays \(0\), then Brian plays \(1\) and wins.
They now decide to change the rules so that Brian wins if, after he plays, the sum of all the numbers played so far is one less than a multiple of \(3\). Again, Amy wins if Brian has not won within five rounds. It is still the case that a player must not repeat the number just played previously.
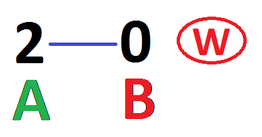
- Show that if Amy starts by playing either \(0\) or \(2\), then Brian can immediately win.
If Amy plays \(0\), Brian plays \(2\) and wins; if Amy plays \(2\), Brian plays \(0\) and wins.
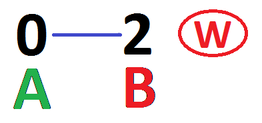
- Suppose, instead, Amy starts by playing \(1\).
Explain why it cannot benefit Brian to play \(2\), assuming Amy plays with the best strategy.
If Amy plays \(1\) and Brian plays \(2\), the game is essentially reset to \(0\) (as \(1+2\) is a multiple of \(3\)).
Amy can then play \(1\) again, leaving Brian in the same position but now with fewer turns to win.
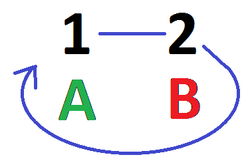
- So suppose Amy starts by playing \(1\), and Brian then plays \(0\). How should Amy play next?
If Amy plays \(1\), Brian can play \(0\) and win, so Amy should play \(2\).
- Assuming both play with the best strategies, who will win the game? Explain your answer.
As shown in the previous parts, the game will start with \((1,0)\; (2,\dots)\;\).
If Brian plays \(0\), the game is essentially reset, with no advantage to him. So Brian’s only chance is to play \(1\).
We then have \((1,0)\; (2,1)\). If Amy plays \(0\), Brian can play \(1\) and win. So Amy’s only chance is to play \(2\).
But we’re now in a cycle, leading to \((1,0)\;(2,1)\;(2,1)\;(2,1)\;(2,1)\), giving a win for Amy; Brian is powerless to stop this.
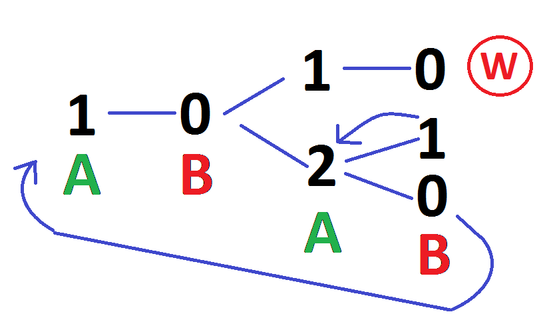
Our conclusion is that if Amy plays with her best strategy, she’ll win.

