Given an \(n\times n\) grid of squares, where \(n>1\), a tour is a path drawn within the grid such that:
- along its way the path moves, horizontally or vertically, from the centre of one square to the centre of an adjacent square;
- the path starts and finishes in the same square;
- the path visits the centre of every other square just once.
For example, below is a tour drawn in a \(6\times6\) grid of squares which starts and finishes in the top-left square.
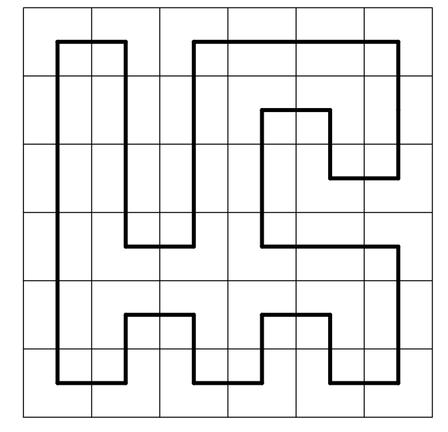
For parts (i)-(iv) it is assumed that \(n\) is even.
With the aid of a diagram, show how a tour, which starts and finishes in the top-left square, can be drawn in any \(n\times n\) grid.
Is a tour still possible if the start/finish point is changed to the centre of a different square? Justify your answer.
Suppose now that a robot is programmed to move along a tour of an \(n\times n\) grid. The robot understands two commands.
- command \(R\) which turns the robot clockwise through a right angle;
- command \(F\) which moves the robot forward to the centre of the next square.
The robot has a program, a list of commands, which it performs in the given order to complete a tour; say that, in total, command \(R\) appears \(r\) times in the program and command \(F\) appears \(f\) times.
Initially the robot is in the top-left square pointing to the right. Assuming the first command is an \(F\), what is the value of \(f\)? Explain also why \(r+1\) is a multiple of \(4\).
Must the results of part (iii) still hold if the robot starts and finishes at the centre of a different square? Explain your reasoning.
Show that a tour of an \(n \times n\) grid is not possible when \(n\) is odd.

