A particular robot has three commands:
- \(\mathbf{F}\): Move forward a unit distance;
- \(\mathbf{L}\): Turn left \(90^{\circ}\);
- \(\mathbf{R}\): Turn right \(90^{\circ}\).
A program is a sequence of commands. We consider particular programs \(P_n\) (for \(n \ge 0\)) in this question. The basic program \(P_0\) just instructs the robot to move forward: \[P_0 = \mathbf{F}.\]
The program \(P_{n+1}\) (for \(n \ge 0\)) involves performing \(P_n\), turning left, performing \(P_n\) again, then turning right: \[P_{n+1}= P_n\, \mathbf{L}\, P_n\, \mathbf{R}.\]
So, for example, \(P_{1} = \mathbf{F\, L\, F\, R}\).
- Write down the program \(P_2\).
- How far does the robot travel during the program \(P_n\)? In other words, how many \(\mathbf{F}\) commands does it perform?
Let the number of \(\mathbf{F}\) commands in \(P_n\) be \(f_n\). Then since \(P_{n+1} = P_n\,\mathbf{L}\,P_n\,\mathbf{R}\), we have \(f_{n+1} = 2f_n\). As \(f_0 = 1\), this gives \(f_n = 2^n\).
- Let \(l_n\) be the total number of commands in \(P_n\); so, for example, \(l_0 = 1\) and \(l_1 = 4\). Write down an equation relating \(l_{n+1}\) to \(l_n\). …
If \(l_n\) is the total number of commands in \(P_n\), then since \(P_{n+1} = P_n\,\mathbf{L}\,P_n\,\mathbf{R}\), we have \[l_{n+1} = l_n + 1 + l_n + 1 = 2l_n + 2.\]
… Hence write down a formula for \(l_n\) in terms of \(n\). No proof is required. Hint: consider \(l_n + 2\).
Let \(L_n = l_n+2\), following the suggestion. Using our formula for \(l_n\), we find \[L_{n+1} = l_{n+1}+2=2l_n+2+2=2L_n,\] and therefore, \[L_n = 2^n L_0.\]
We are given \(l_0 = 1\), so \(L_0 = 3\), so \[L_n = 3 \times 2^n.\]
Then as \(l_n=L_n-2\), we get \[l_n = 3 \times 2^n - 2.\]
Check: for \(n=2\), this gives \(l_2=3\times4-2=10\), which tallies.
- The robot starts at the origin, facing along the positive \(x\)-axis. What direction is the robot facing after performing the program \(P_n\)?
Since \(P_0\) contains only an \(\mathbf{F}\), we see that each program \(P_n\) contains an equal number of \(\mathbf{L}\) and \(\mathbf{R}\) commands.
Therefore the robot will still face along the positive \(x\)-axis after completing \(P_n\).
The first diagram below shows the path the robot takes when it performs the program \(P_1\). On the second (blank) diagram, draw the path it takes when it performs the program \(P_4\).


It helps to work out the paths for \(P_2\) and \(P_3\).
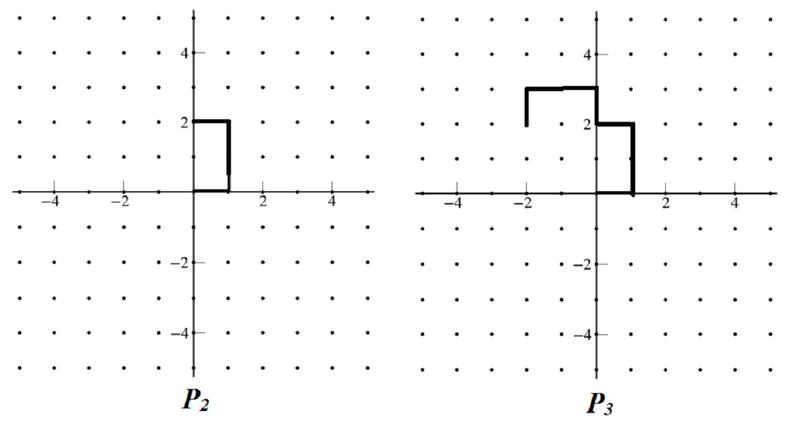
To find \(P_3\), we do \(P_2\), then turn to north and repeat \(P_2\).
To find \(P_4\), we do \(P_3\), then turn to north and repeat \(P_3\). This gives us

Four copies of \(P_2\) are clearly visible, as are 8 copies of \(P_1\).
- Let \((x_n, y_n)\) be the position of the robot after performing the program \(P_n\), so \((x_0, y_0) = (1,0)\) and \((x_1, y_1) = (1,1)\). Give an equation relating \((x_{n+1}, y_{n+1})\) to \((x_n, y_n)\).
We have the relationship \[P_{n+1} = P_n\,\mathbf{L}\,P_n\,\mathbf{R}.\]
Originally the robot is at the origin facing east. Performing \(P_n\) takes the robot to \((x_n,y_n)\) still facing east.
The move \(\mathbf{L}\) turns the robot left \(90^\circ\), so it then faces north.
Now imagine the robot is at the origin but facing north. Performing \(P_n\) moves the robot to position \((-y_n, x_n)\).
So facing north and performing \(P_n\) will translate the robot by the vector \(\dbinom{-y_n}{x_n}\).
So starting at the origin and facing east, after performing \(P_n\,\mathbf{L}\,P_n\), the robot will be at position \((x_n - y_n, y_n + x_n)\).
This position is obviously unchanged by performing the final \(\mathbf{R}\).
Therefore \[(x_{n+1},y_{n+1}) = (x_n - y_n, x_n + y_n).\]
What is \((x_8, y_8)\)? What is \((x_{8k}, y_{8k})\)?
Setting \(n=0\) in the final expression gives \[(x_8, y_8) = (16x_0, 16y_0) = (16,0),\] and we can also see from the final expression that \[(x_{8k}, y_{8k}) = (16^k,0).\]
The program Logo is perfect for trying out programs involving F, L and R. Search on the internet to find a free download.

