A magic square is a square grid in which the numbers in each row, column and diagonal sum to the same number.
For example,
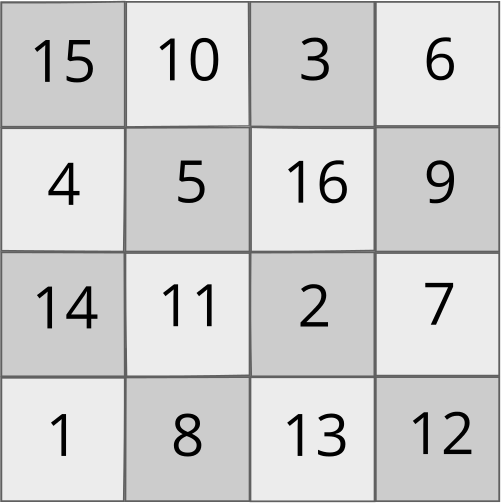
is a magic square that uses each of the numbers from \(1\) to \(16\) once.
There are many of magic squares of different sizes; perhaps you have come across some. The artist Albrecht Dürer even included one in his engraving Melancholia I.
But why are magic squares about addition? Could we have a magic square where the numbers in each row, column and diagonal multiply to the same number?
Suppose we have a \(7\) in a row of a multiplication magic square. What does that tell us?
There’s more than one way to think about this, so here’s a suggestion towards another approach.
How might we turn a problem about multiplication into a problem about addition, or vice versa?

