- Suppose that \(a\), \(b\) and \(c\) are integers that satisfy the equation \[a^3 + 3b^3 = 9c^3.\]
Explain why \(a\) must be divisible by \(3\), and show further that both \(b\) and \(c\) must also be divisible by \(3\). Hence show that the only integer solution is \(a = b = c = 0\).
We have \[a^3 = 9c^3 - 3b^3 = 3(3c^3 - b^3),\] so \(a^3\) is a multiple of \(3\).
Now if \(3\) does not divide \(a\), it does not divide \(a^3\), so \(3\) must divide \(a\). Thus we can write \(a = 3d\), where \(d\) is an integer, and we have \[(3d)^3 + 3b^3 = 9c^3,\] which, on dividing by \(3\), gives \[9d^3 + b^3 = 3c^3.\]
By the same argument, as \[b^3 = 3(c^3 - 3d^3),\] it follows that 3 divides \(b^3\), and also \(b\). We repeat the same trick, writing \(b = 3e\), where \(e\) is an integer, so that \[9d^3 + (3e)^3 = 3c^3.\]
We again divide by \(3\) to get \[3d^3 + 9e^3 = c^3,\] so that 3 divides \(c^3\), and also \(c\). We then write \(c = 3f\), where \(f\) is an integer, giving \[3d^3 + 9e^3 = (3f)^3.\]
Finally, we divide this equation by \(3\) to get \[d^3 + 3e^3 = 9f^3.\]
Now this is the same equation that we started with. So if \(a\), \(b\), \(c\) are integers which satisfy the equation, then so are \(d = \dfrac{a}{3}\), \(e = \dfrac{b}{3}\) and \(f = \dfrac{c}{3}\).
Thus from our imagined starting solution \((a,b,c)\), if \((a,b,c)\) is not \((0,0,0)\), we have constructed a smaller integer solution \((d,e,f)\).
We could repeat this process indefinitely, but there are only finitely many integers smaller than \(a\); a contradiction!
The only way out is if \((a,b,c) = (0,0,0)\), when \((d,e,f)\) is not a smaller solution, but is \((0,0,0)\) also.
More precisely once again…
if \(a\), \(b\), \(c\) are integers which satisfy the equation, then so are \(d = \dfrac{a}{3}\), \(e = \dfrac{b}{3}\) and \(f = \dfrac{c}{3}\), so that for any \(n\), the numbers \(\frac{a}{3^n}\), \(\frac{b}{3^n}\) and \(\frac{c}{3^n}\) are also integers which satisfy the equation.
But if \(\frac{a}{3^n}\) is an integer for all \(n \ge 0\), we must have \(a = 0\), and similarly for \(b\) and \(c\).
Therefore the only integer solution is \(a = b = c = 0\).
- Suppose that \(p\), \(q\) and \(r\) are integers that satisfy the equation \[p^4 + 2q^4 = 5r^4.\]
By considering the possible final digit of each term, or otherwise, show that \(p\) and \(q\) are divisible by \(5\). Hence show that the only integer solution is \(p = q = r = 0\).
We are interested in the equation \(p^4 + 2q^4 = 5r^4.\)
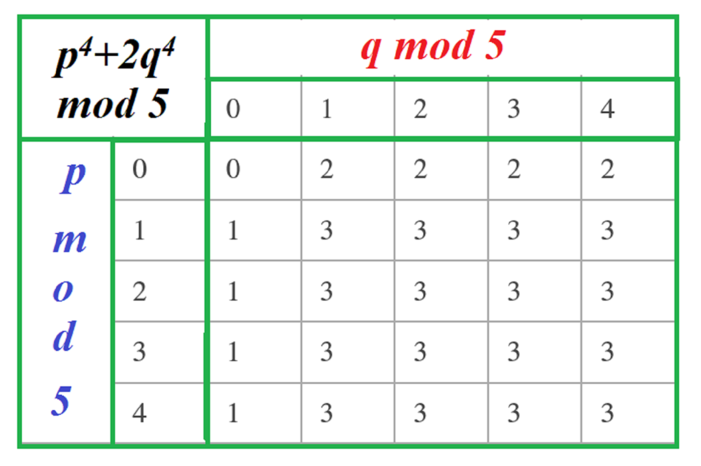
This table gives \(p^4 + 2q^4 \mod 5\), that is, the remainder when \(p^4 + 2q^4\) is divided by 5.
The only way \(p^4 + 2q^4\) can be \(0\) mod \(5\) is if \(p = 0 \mod 5\), and \(q = 0 \mod 5\), in other words, if \(5\) divides both \(p\) and \(q\).
Now as in part (i), we write \(p = 5a\) and \(q = 5b\), where \(a\) and \(b\) are both integers, to get \[(5a)^4 + 2(5b)^4 = 5r^4.\]
Dividing both sides by \(5\) gives \[5^3a^4 + 2(5^3b^4) = r^4,\]
so as before, \(r^4\) must be a multiple of \(5\), and since \(5\) is prime, \(r\) must be a multiple of \(5\). Then writing \(r = 5c\) gives \[5^3a^4 + 2(5^3b^4) = (5c)^4,\] which yields \[a^4 + 2b^4 = 5c^4\] on dividing by \(5^3\).
So once again, if \(p\), \(q\), \(r\) give an integer solution to the equation, then so do \(a = \dfrac{p}{5}\), \(b = \dfrac{q}{5}\) and \(c = \dfrac{r}{5}\). Repeating this, so are \(\dfrac{p}{5^n}\), \(\dfrac{q}{5^n}\), \(\dfrac{r}{5^n}\) for any integer \(n \geq 0\), and as before, this shows that the only integer solution is \(p = q = r = 0\).
The type of argument used here (using one imagined solution to find a smaller one) is known as infinite descent, which was popularised by Pierre de Fermat.

