A triomino is a flat L shape made from three square tiles.

A board is divided into squares the same size as the tiles. The board is \(2^n\) by \(2^n\) squares.
One square, anywhere on the board, is coloured blue.
We can put triominoes on the board, but they must not overlap and must not cover the blue square.
Is it possible to cover the board (apart from the blue square) with triominoes? Does it depend on where the blue square is, or on the \(n\) that determines the size of the board? Justify your answer.
We shall show that for any \(n \geq 1\) and any position of the blue square, it is possible to cover the rest of the board with triominoes.
\(n = 1\)
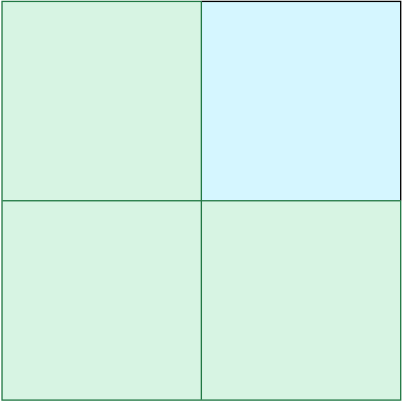
When \(n = 1\), we have a \(2\) by \(2\) board, and one of the squares is blue.

It doesn’t matter which square is blue, because we can rotate the board until the blue square is in the top right. We might say that “Without loss of generality, the top right square is blue”.
Then the remaining squares form a triomino, so of course can be covered by a triomino.
\(n = 2\)
When \(n = 2\), we are considering a \(4\) by \(4\) board.
We could now think about the various possible places for the blue square, and show that in each case we can cover the board with triominoes, but that strategy is not going to generalise well to larger values of \(n\): we would rapidly end up with too many cases. Fortunately, there is another way to think about it.
We can think of the \(4\) by \(4\) board as being made up of four \(2\) by \(2\) boards.
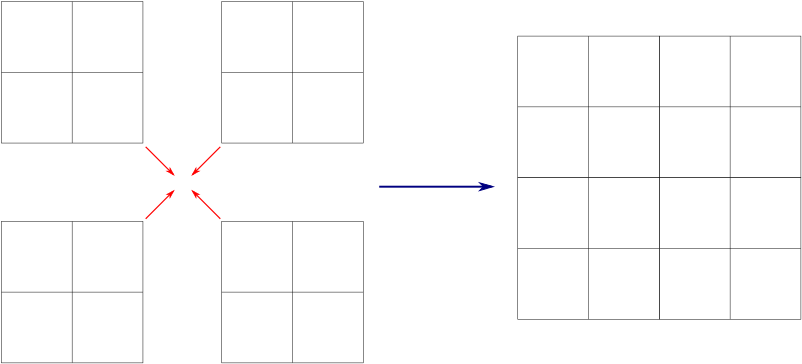
The blue square must lie in one of those \(2\) by \(2\) boards. We already know that we can cover the rest of that \(2\) by \(2\) boards with triominoes—that was the case we did above. That leaves a giant L shape that we want to cover with triominoes.
There are a couple of ways of thinking about this. We’ll do both, and then think about how they transfer to larger boards.
Approach 1
We have three \(2\) by \(2\) boards forming an L shape. We can take a square out of each of them and colour it pink, and as above we can then cover the remaining parts of the boards with triominoes. Let’s choose the pink squares to be the ones nearest the centre of the original \(4\) by \(4\) board.
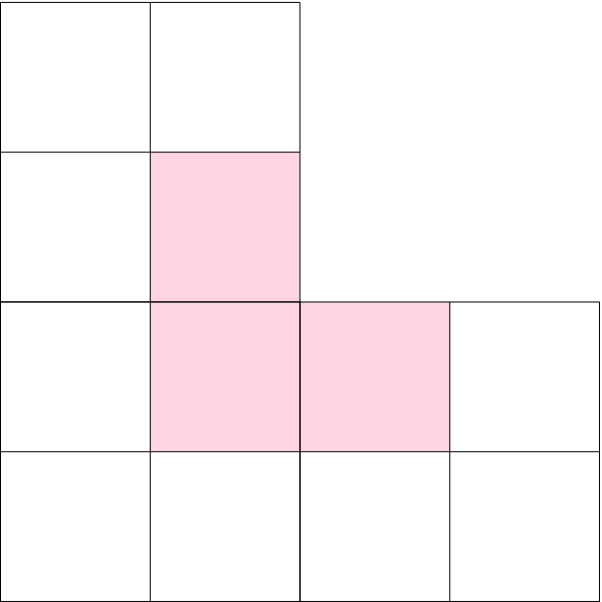
Then we can cover the pink squares with a triomino, and so we can cover the whole shape with triominoes.
Approach 2
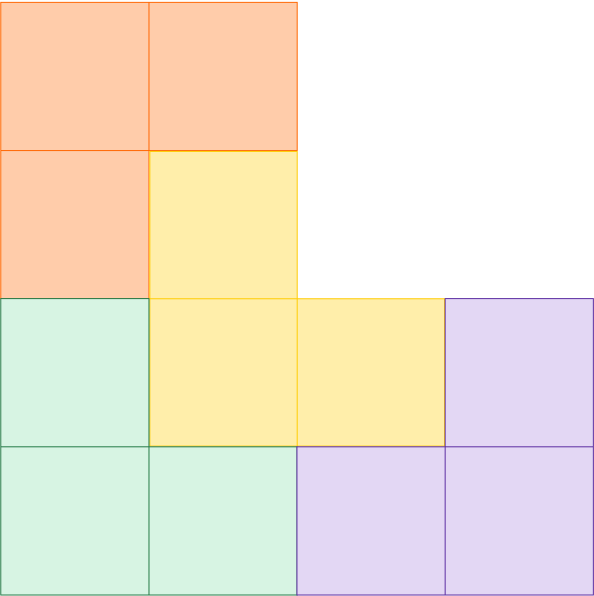
Let’s call a basic triomino a \(1\)-triomino, to record the fact that it’s \(1\) square thick. Then the L shape made of three \(2\) by \(2\) boards is a \(2\)-triomino, and we can cover it with \(1\)-triominoes as shown.
\(n = 3\)
Let’s try to use the same strategy as for the \(4\) by \(4\) board, and see how far we can get. We’ve had a good idea, so we should make the most of it!
We have an \(8\) by \(8\) board, which we can think of as being made up of four \(4\) by \(4\) boards. The blue square must be in one of those boards, and as above we know that we can then cover the rest of that board with triominoes. That then leaves a large L shape made up of three \(4\) by \(4\) boards.
Approach 1
We can take one square from each \(4\) by \(4\) board, around the centre of the original \(8\) by \(8\) board, and colour them pink.

We can cover the pink squares with a single triomino. And we can cover the remainder because we know that we can cover a \(4\) by \(4\) board with one square removed. So we can cover the whole board.
Approach 2
We have a \(3\)-triomino. We can cover that with \(2\)-triominoes, in the same way that we can cover a \(2\)-triomino with \(1\)-triominoes.

That is, we can cover a \(3\)-triomino with \(2\)-triominoes, and we already know that we can cover \(2\)-triominoes with \(1\)-triominoes, so we can cover a \(3\)-triomino with \(1\)-triominoes.
And so on…
We can continue in the same way. For example, to show that we can cover a \(64\) by \(64\) board, we’d use the fact that we can cover a \(32\) by \(32\) board and one of the approaches described above, and in turn to reach the \(32\) by \(32\) board we’d use a \(16\) by \(16\) board, and then back to \(8\) by \(8\).
To make this more formal, we can use proof by induction, which captures the above “and so on” in a more precise way. Here’s one way of phrasing the argument using induction, but you should think of it as taking the above argument and phrasing it more concisely—the maths is the same.
Proof by induction
Base case \(n = 1\): Without loss of generality, we may assume that the blue square is in the top right corner (if not, rotate the board until it is).

It is then clear that we can cover the rest of the board with a single triomino.

Induction step: Suppose that we know that we can cover a \(2^k\) by \(2^k\) board with any one square coloured blue. For Approach 2, if \(k>1\), we also suppose that we can cover a \((k-1)\)-triomino with \(1\)-triominoes.
Secret aim: Show that we can cover a \(2^{k+1}\) by \(2^{k+1}\) board with any one square coloured blue, and if we are using Approach 2, then we also show that we can cover a \(k\)-triomino with \(1\)-triominoes.
Consider a \(2^{k+1}\) by \(2^{k+1}\) board. We may think of this as being made up of four \(2^k\) by \(2^k\) boards.

Without loss of generality the blue square is in the top right \(2^k\) by \(2^k\) board. By the inductive hypothesis, we can then cover the rest of this board with triominoes.
We still need to show that we can cover the remaining L shape, made of three \(2^k\) by \(2^k\) boards.
Approach 1
Colour one square of each board pink, choosing the squares nearest the centre of the original \(2^{k+1}\) by \(2^{k+1}\) board as shown.

We can cover the pink squares with a single triomino. We are left with three \(2^k\) by \(2^k\) boards, each with a single square removed, and by the induction hypothesis we can cover each of those with triominoes.
Approach 2
We have a \(k\)-triomino that we want to cover. But we can cover it using \((k-1)\)-triominoes:

and if \(k-1>1\), then by the inductive hypothesis we can cover a \((k-1)\)-triomino using \(1\)-triominoes, so we can cover a \(k\)-triomino with \(1\)-triominoes.
Whether we use Approach 1 or Approach 2, we see that if we can cover a \(2^k\) by \(2^k\) board then we can cover a \(2^{k+1}\) by \(2^{k+1}\) board.
So we are done by induction.

