Here are two possible approaches to solving the equations.
Method 1
For the first pair, subtract the second equation from the first to obtain \[0.00001x - 0.00001y = 0.00001.\] Dividing through by \(0.00001\) then gives \[x - y = 1.\] We can now add this to the second initial equation to eliminate \(y\); we get \[1.99999x = 3.99998.\] Now dividing through by \(1.99999\) gives \[x = 2,\] and so also \[y = 1.\]
For the second pair, we can again subtract the second equation from the first, which this time gives \[0.00001x + 0.00001y = 0.00001.\] Dividing through then gives \[x + y = 1.\] Subtracting the second initial equation from this (to eliminate \(y\)) gives \[0.00001x = -1.99998,\] and so \[x = - 199998,\] which in turn leads to \[y = 199999.\]
Method 2
For the first system, multiply the second equation by \(0.99999\) and subtract it from the first one. We see \[(1 - 0.99999^2)x = 2.99999 - 2.99998 \times 0.99999,\] which implies that \[x = \frac{2.99999 - 2.99998 \times 0.99999}{1 - 0.99999^2} = \frac{0.0000399998 }{0.0000199999} = 2,\] so finally substituting back into either equation we obtain \[x=2, \qquad y = 1.\]
For the second system, multiply the second equation by \(1.00001\) before subtracting it from the first. We get \[x = \frac{2.99999 - 2.99998 \times 1.00001}{1 - 1.00001\times 0.99999} = \frac{-0.0000199998}{0.0000000001} = -199998,\] and so \[y = 199999.\]
Explain why the solutions are so different and yet the pairs of equations are nearly identical.
One helpful way to explain this is geometrically. We can view the problem of solving these equations as being the problem of finding the intersections of pairs of lines.
Both pairs of lines are very nearly parallel, but the second pair are much closer to being parallel—even though the difference in their offsets is only a little smaller than that for the first pair.
Because nearly parallel lines approach each other only very slowly, the pair which is much closer to being parallel takes much longer to meet when starting from the origin.
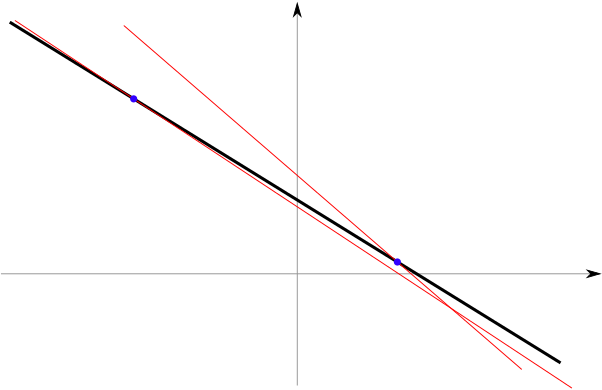
By only very slightly changing the slope (and intercept if we like) of the first line, the point at which the intersection lies can be moved enormous distances. In particular, because two distinct parallel lines never meet, we can make the intersection as far away as we like by slowly tuning the slopes to the same value!
Also, note that in both pairs of equations, the first line is steeper. That said, in the first pair the first line is higher at \(x=0\) whilst in the second pair, the second line is on top at \(x=0\). This explains the difference in the sign of the solutions \(x\).
A more algebraic approach might involve solving the system more generally. Here is such an argument.
as our system of equations. Then focusing on \(x\), we find (assuming \(d \neq 0\)) \[\left(a - \frac{b}{d} c\right) x = e - \frac{b}{d} f\] or (assuming \(ad-bc \neq 0\)) \[x = \frac{d e - b f}{ad-bc}.\] Now changing \(a\), \(b\), \(c\), \(d\), \(e\), \(f\) in the original equations a little corresponds to changing the numerator and denominator slightly. So now the question we’re interested in is simply whether \(x = \frac{p}{q}\) can change dramatically when we change \(p\) and \(q\) only a little—we are investigating the solutions to \[qx = p.\]
In fact, the solution \(x\) certainly can be very sensitive, because if \(q\) is very small then \(1/q\) is very large, and even small changes in \(q\) give rise to enormous ones in \(1/q\). For instance, we have \[\frac {1}{0.001} = 1000, \qquad \frac {1}{0.000001} = 1000000, \qquad \frac {1}{-0.001} = -1000.\]
Indeed, we can check \(ad-bc\) for the equations is very close to zero, which explains how sensitive the solution is to small changes of the parameters: we have \[ad-bc = 0.0000199999\] for the first pair, and \[ad-bc = 0.0000000001\] for the second pair.
As an aside, notice that \(q=0\) is the point around which things become very sensitive in solving \(qx=p\), which is exactly where the equation might have no solution (or infinitely many solutions).
Similarly, \(ad-bc = 0\) is exactly the point at which the original pair of equations have either no solution or infinitely many solutions. You might like to try to construct simple examples of equations with both zero and infinitely many solutions.
You might like to read this short piece about the butterfly effect.

