In the triangle \(ABC\) the equations of two of the sides are \(2y=x+2\) and \(y=2x-2\). Given that \(A\) is the point \((4,3)\) and that \(A\hat{B}C\) is \(90^\circ\), find the equation of the third side.
Our best starting plan is to draw a diagram.
The point \(A\) must be on either \(y = 2x-2\), or \(2y = x + 2\), and we can see by substituting in that \(A\) is on the second of these but not the first.
So the first line (\(y=2x-2\)) must give the side \(BC\), so \(B\) lies on this line. We are also told that the angle at \(B\) is a right angle.
We can now sketch our diagram. (At this stage, we have not worked out whether \(2y=x+2\) passes through \(B\) or not.)
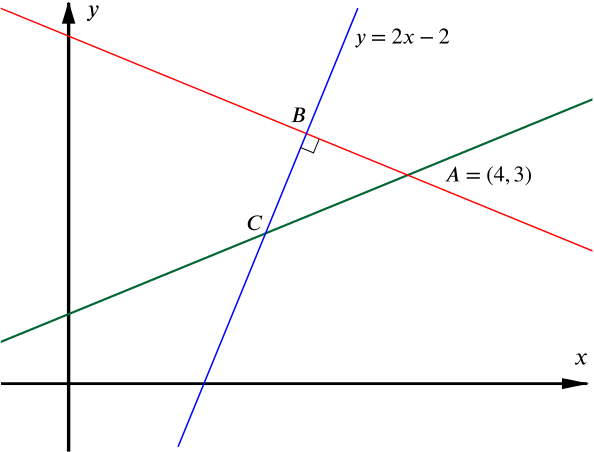
Now the gradient of \(BC\) is \(2\), so the gradient of \(AB\) is \(-\frac12\), since \(AB\) is perpendicular to \(BC\). Since the line \(AB\) passes through \(A(4,3)\), it follows that it has equation \(y-3=-\frac12(x-4)\) (using the general formula \(y-y_1=m(x-x_1)\)), which rearranges to \(y=-\frac12x+5\) or \(x+2y=10\). This is the equation of the third side.
It also follows that \(2y=x+2\) is the line \(AC\) (since it has gradient \(+\frac12\), so is not perpendicular to \(BC\)). This would allow us to work out the coordinates of \(C\), though we are not asked to find these.

