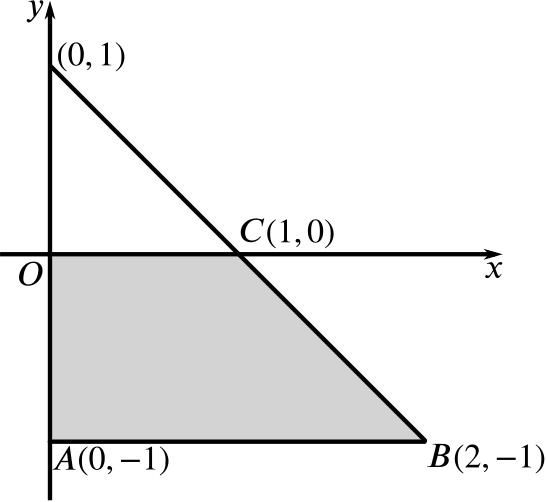
\(O\) is the origin and \(A\), \(B\) and \(C\) are the points \((0,-1)\), \((2,-1)\) and \((1,0)\) respectively. Write down the four inequalities which define the shaded region \(ABCO\) including its boundary.
The shaded region is bounded by four lines: \(y=0\), \(x=0\), \(y=-1\) and by the straight line through \((0,1)\), \((1,0)\) and \((2,-1)\).
Writing this straight line as \(y=mx+c\), we know that \(c=1\), since \(c\) is the \(y\)-intercept. We know the point \((1,0)\) is on the line, so \(0=m+1\), which means the fourth line segment bounding the shaded area is part of \(y=1-x\).
Since the shaded area is below the \(x\)-axis, the first inequality is \[y\le 0,\] since we wish to include the boundary of the shaded area.
Since the shaded area is to the right of the \(y\)-axis, the second inequality is \[x\ge 0.\] The shaded region is above the line \(y=-1\), so the third equation is \[y\ge-1.\]
Which side of the line \(y = 1-x\) do we want? We want the side that includes the origin. When \(x = 0\) and \(y = 0, y < 1-x\), so this is the side we want.
So the fourth and final inequality is \[y\le 1-x.\]

