The sum and product of two numbers, \(x\) and \(y\), are \(10\) and \(12\) respectively. Form appropriate equations, plot [on graph paper] the corresponding graphs and hence obtain approximate values for \(x\) and \(y\).
The following graph shows both the line (corresponding to the first equation) and the hyperbola (corresponding to the second equation).
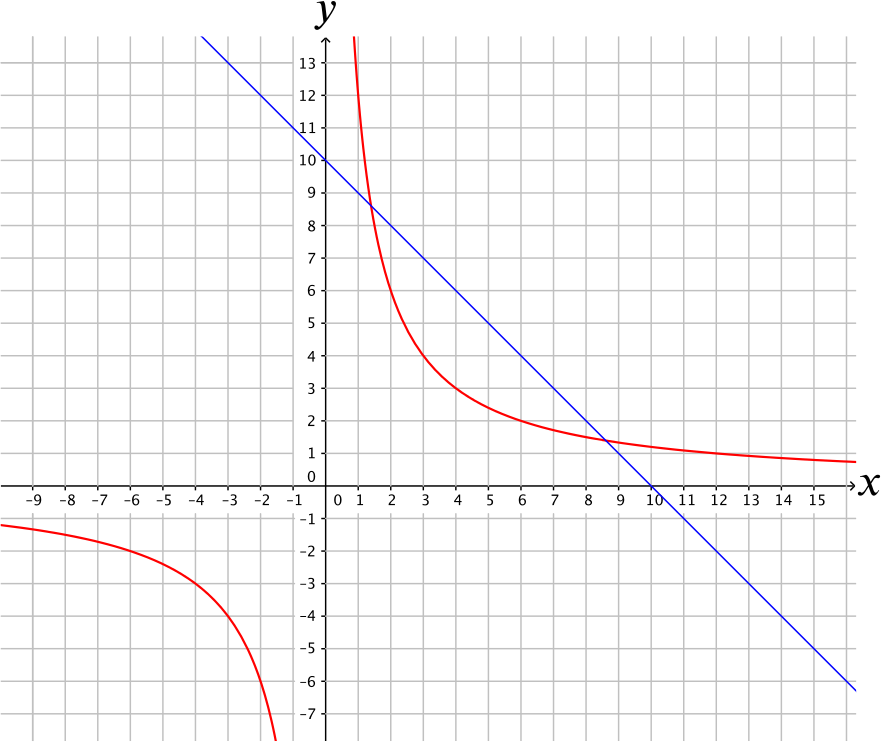
The graph shows that there is an approximate solution with \(x \approx 1.4\) and \(y \approx 8.6\) and another one with \(x \approx 8.6\) and \(y \approx 1.4\). These give essentially the same solution, as we are looking for two numbers with a given sum and given product.
The equations can be solved exactly, and without much difficulty. By substituting the equation \(y = 10 - x\) into the equation \(xy = 12\), we have \[x(10 - x) = 12\] so that \[x^2 - 10x + 12 = 0.\] By the quadratic formula, we have that
\[\begin{align*}
x &= \frac{10 \pm \sqrt{(-10)^2 - 4 \cdot 1 \cdot 12}}{2 \cdot 1} \\
&= \frac{10 \pm \sqrt{100 - 48}}{2} \\
&= \frac{10 \pm \sqrt{52}}{2}.
\end{align*}\]
The smaller of these values is \(1.394448\!\ldots\), which is close to our visual estimate.
