The points \(A(1,2)\) and \(B(-2,1)\) are two vertices of a rectangle \(ABCD\). The diagonal \(CA\) produced passes through the point \((2,9)\). Calculate the coordinates of the vertices \(C\) and \(D\).
Let’s draw a diagram to help us visualise the question.
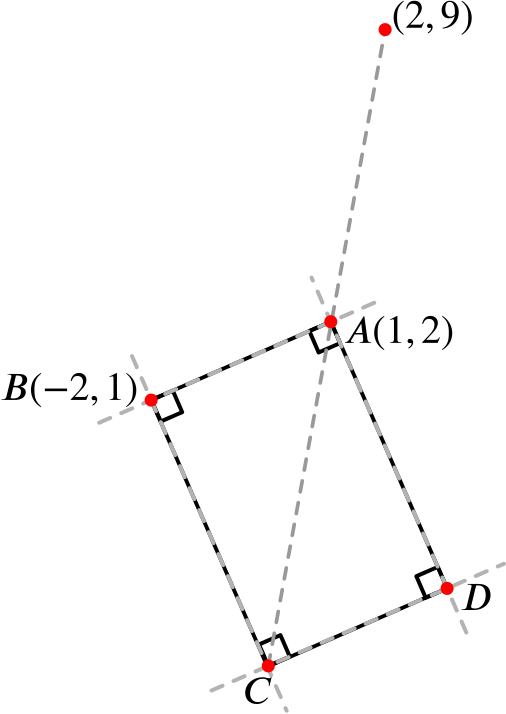
The point \(A\) has coordinates \((1,2)\) and \(B\) has coordinates \((-2,1)\), so the gradient of \(AB\) is \[\frac{\text{change in $y$}}{\text{change in $x$}}=\frac{2-1}{1-(-2)}=\frac{1}{3}.\]
Now we know that the line \(BC\) will be perpendicular to \(AB\), and so will have gradient \(-3\). As it passes through \(B(-2,1)\), it has equation \(y-1=-3(x+2)\) (using the general formula \(y-y_1=m(x-x_1)\)), which we can rearrange to obtain \[y=-3x-5.\]
In order to find \(C\), we must find where \(BC\) intersects the line \(AC\), whose equation we can find since we know two points on it, \((1,2)\) and \((2,9)\). The gradient of this line is then \[\frac{9-2}{2-1}=7,\] and so it has equation \(y-2=7(x-1)\), or \(y=7x-5\).
So to find \(C\) we must find where \(AC\) meets \(BC\), i.e., where \(y=7x-5\) and \(y=-3x-5\) meet. We see that \[7x-5=-3x-5,\] from which we obtain \(x=0\), and so \(C\) is the point \((0,-5)\).
Finally, we need to find the coordinates of \(D\). To get from \(B\) to \(A\), we move right \(3\), up \(1\). So if we go right \(3\), up \(1\) from \(C\), we get to \(D\), which therefore has coordinates \((3, -4)\).
We can think of “to get from \(B\) to \(A\)” as the vector \(\overrightarrow{BA}=\dbinom{3}{1}\), so the final sentence could be rewritten as:
As \(\overrightarrow{BA}=\dbinom{3}{1}\) and \(\overrightarrow{CD}=\overrightarrow{BA}\), we see that \(D\) has coordinates \((3,-4)\).

