\(X\) is a fixed point \((3,0)\), \(Y\) is the point \((0,a)\). A line is drawn through \(Y\) and perpendicular to \(XY\), meeting the \(x\)-axis at \(Q\). On this line a point \(P\) is taken so that \(Y\) is the mid-point of \(QP\). Find the coordinates of \(P\).
We begin by sketching a graph of the situation.
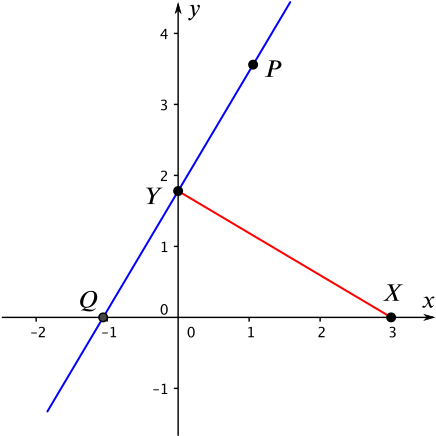
Our strategy is now clear: we will find the gradient of the line \(XY\), and so be able to work out the gradient of \(PQ\). This will allow us to find the equation of \(PQ\), and hence the coordinates of \(Q\). Since \(Y\) is the midpoint of \(PQ\), we will then be able to find the coordinates of \(P\).
The gradient of the line segment \(XY\) is \[\frac{a-0}{0-3} = -\frac{a}{3}.\] Provided that \(a \ne 0\), the equation of any line perpendicular to \(XY\) must therefore have a gradient equal to \(\dfrac{3}{a}\). (We will deal with \(a=0\) later on as a special case.)
So the equation of the line with gradient \(\dfrac{3}{a}\) that passes through \(Y(0,a)\) is \[y = \dfrac{3}{a} x + a,\] since the \(y\)-intercept is \(a\).
The point where this line intersects the \(x\)-axis (\(y=0\)) has \(x\)-coordinate \(-\dfrac{a^2}{3}\), so the point \(Q\) has coordinates \(\left( -\dfrac{a^2}{3}, 0 \right)\).
To get from \(Q\) to \(Y\) we go \(\dfrac{a^2}{3}\) to the right, then \(a\) up, so we need to repeat this to get to \(P\), which is therefore the point \(\left(\dfrac{a^2}{3}, 2a \right)\).
It is also clear from the sketch that the \(x\)-coordinates of \(P\) and \(Q\) are negatives of each other, and that the \(y\)-coordinate of \(Q\) is twice the \(y\)-coordinate of \(Y\).
In the case that \(a = 0\), the points \(Y, Q\) and \(P\) coincide at the origin. So for all values of \(a\), the point \(P\) can be expressed as \(\left( \dfrac{a^2}{3}, 2a \right)\).
Is this still true if \(a<0\)?
Find the equation of the locus of \(P\) for varying values of \(a\).
We need to determine the locus of the point \(P\left( \dfrac{a^2}{3}, 2a \right)\) as \(a\) varies.
If \(x = \dfrac{a^2}{3}\) and \(y = 2a\), then \(a = y/2\), giving \(x = \dfrac{(y/2)^2}{3}\). Rearranging yields \(y^2 = 12x\), which is the equation of a parabola which is symmetrical about the \(x\)-axis.

This GeoGebra applet can help us to see what is going on.

