Find
- the equation of the line with gradient \(-2\) which passes through the point \((2t,t)\),
Using the general formula \(y-y_1=m(x-x_1)\), the equation is \(y-t=-2(x-2t)\), which rearranges to give \(y=-2x+5t\) or \(2x+y=5t\).
Find
- the values of \(t\) for which the area enclosed by this line and the coordinate axes is \(4\) square units.
We begin by finding the points where this line intersects the axes.
When \(x=0\), \(y=5t\), and when \(y=0\), \(x=\frac52 t\), so the points of intersection are \((0,5t)\) and \((\frac52 t,0)\). A sketch of the situation looks like this; we have drawn two sketches, one for the case \(t>0\) and the other for the case \(t<0\).
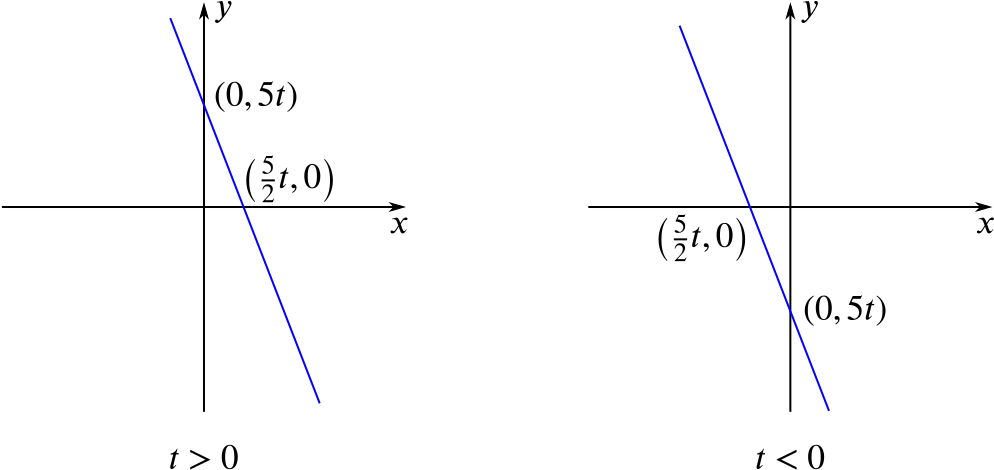
The region enclosed by the line and the coordinate axes is a right-angled triangle, so its area is given by \[\text{area} = \frac{1}{2} \times \frac{5}{2}t \times 5t = \frac{25}{4}t^2.\]
We are asked to find the values of \(t\) for which this area equals \(4\), so we need \[\frac{25}{4}t^2 = 4.\] This gives \(t^2=\frac{16}{25}\) and so \(t = \pm \frac{4}{5}\).
We have not been quite precise in this argument. The area is \(\frac{1}{2} \times \frac{5}{2}t \times 5t=\frac{25}{4}t^2\) when \(t\) is positive, but when \(t\) is negative, the side lengths (which must be positive) are \(-\frac52 t\) and \(-5t\), so the area is then \(\frac{1}{2} \times \bigl(-\frac{5}{2}t\bigr) \times (-5t)\). However, this still multiplies to give \(\frac{25}{4}t^2\), so our final answer is correct, as can also been seen by the symmetry of the situation.

