Describe and indicate by shading, on the usual axes, the set of points \(S_1\) defined by \((x-2)(y+3) \geq 0\).
The boundary of the region is given by \((x-2)(y+3)=0\), so either \(x=2\) or \(y=-3\). So \(S_2\) is bounded by two straight lines.
We have \((x-2)(y+3) \geq 0\) when either \(x-2\geq 0\) and \(y+3 \geq 0\), or \(x-2\leq 0\) and \(y+3 \leq 0\). Alternatively, we could pick a point in each of the four regions formed by the two straight lines to determine whether or not it is in \(S_1\). For example, \((0,0)\) has \((0-2)(0+3)=-2<0\), so the origin does not lie in \(S_1\).
Using either approach, we deduce that \(S_1\) is the shaded region in this diagram:

The boundary of the region (the lines \(x = 2\) and \(y = -3\)) is included in \(S_1\).
\(S_2\) is the set of points defined by \(x^2 + y^2 \leq 25\). Find the range of values of \(p\) if the point \((3, p) \in S_1 \cap S_2\).
The set \(S_2\) is the interior and boundary of a circle centred on the origin with radius \(5\).
Thus the intersection of \(S_1\) and \(S_2\) (the points in both \(S_1\) and \(S_2\)) is the area of overlap:
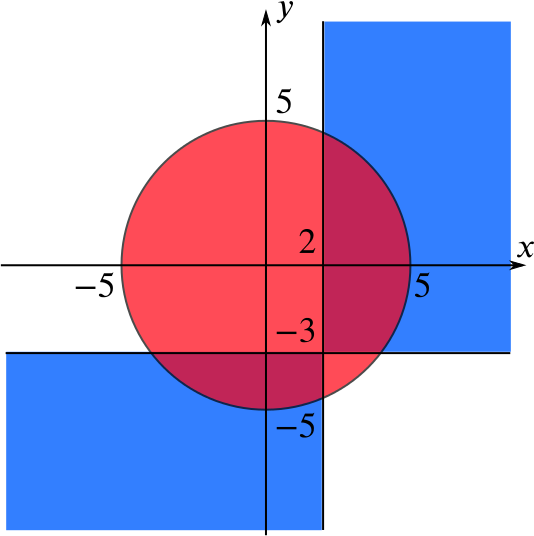
Thus the range of values of \(p\) if the point \((3, p) \in S_1 \cap S_2\) is given by the \(y\)-coordinates of the points in the intersection of the overlap region with the line \(x = 3\):
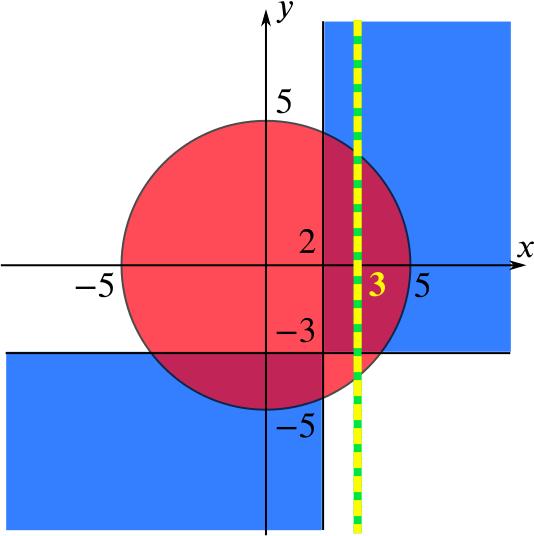
It’s easy to see that the line \(x=3\) leaves the overlap region at \((3,4)\) (since this is on the circle) and at \((3,-3)\) (which is on the line \(y=-3\)), and both of these points are included, so \(-3 \leq p \leq 4\).

