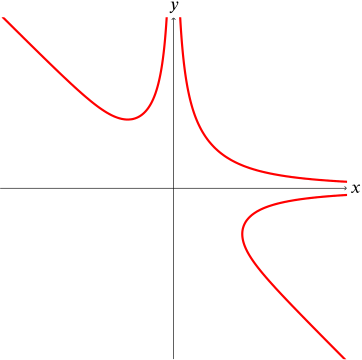
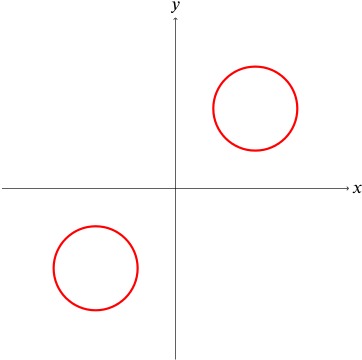
A sketch of the curve with equation \(x^2y^2(x+y)=1\) is drawn in which of the following diagrams?
| (a) |

|
(b) |

|
| (c) |
|
(d) |
|
Firstly, we can rule out options (a) and (b) because points which satisfy \(x^2y^2(x+y)=1\) cannot have \(x=0\) or \(y=0\). Since graphs (a) and (b) both cross the axes, these cannot give the correct solution.
Now let’s rearrange the equation of the curve. We have \[x+y=\frac{1}{x^2y^2}>0\] so points on the curve must lie only in regions where \(x+y>0\), or \(y>-x\). This rules out option (d).
Hence, by process of elimination, (c) is the correct answer.
Alternatively, can we have \(x=y\:\)? We can, but only where \(x=y=2^{-1/5}>0\). Graphs (a) and (b) show no such point, while graph (d) seems to show \(4\) of them. Hence the answer must be (c).

