Given that \(A\) is the point \((0,3)\) and \(B\) is the point \((0,-3)\), a point \(P(x,y)\) moves so that \(PA=2PB\). Show that the equation of the locus of \(P\) is \[ x^2 + y^2 +10y + 9 = 0.\]
as seen in this sketch:
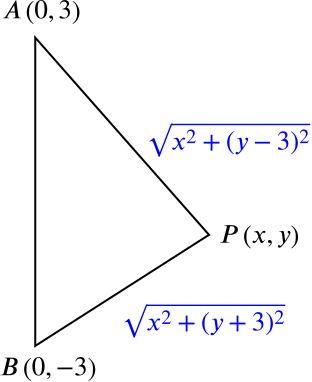
We can now insert the expressions for \(PA\) and \(PB\) into the constraint \(PA=2PB\), giving \[\sqrt{x^2 + (y-3)^2} = 2\sqrt{x^2 + (y+3)^2}.\]
Next, we square both sides and expand the brackets. We have
\[\begin{align*} &&\sqrt{x^2 + (y-3)^2} &= 2\sqrt{x^2 + (y+3)^2}&&\quad\\ \implies\quad&& x^2 + (y-3)^2 &= 4x^2 + 4(y+3)^2\\ \implies\quad&& x^2 + y^2-6y+9&=4x^2+4y^2+24y+36. \end{align*}\]Collecting like terms gives \[3x^2 + 3y^2 + 30y + 27 = 0\] which, on dividing by \(3\), gives the equation of the locus of \(P\) in the form requested, namely \(x^2 + y^2 +10y + 9 = 0\).
A more general problem with detailed suggestions and solutions can be found in The Circle of Apollonius.

