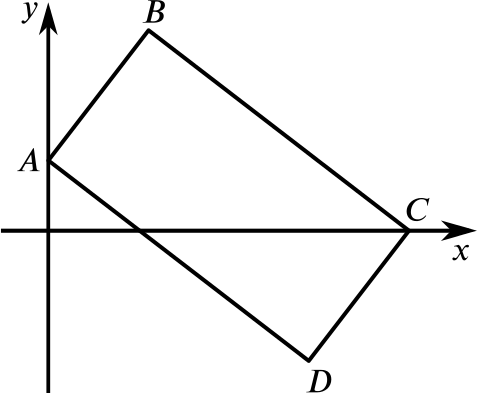
The diagram shows a parallelogram \(ABCD\) with \(A\) and \(C\) on the coordinate axes. The equation of \(AB\) is \(y=2x+1\) and the equation of \(BC\) is \(2y+x=12\).
- Show that \(ABCD\) is a rectangle.
Since \(ABCD\) is a parallelogram, we just need to check that \(AB\) and \(BC\) are perpendicular.
The equation of \(AB\) is \(y=2x+1\), which has gradient \(2\), and the equation of \(BC\) is \(2y+x=12\), or \(y=6-\frac{1}{2}x\) and so the gradient of \(BC\) is \(-\frac{1}{2}\).
Since \(2\times -\frac{1}{2}=-1\), \(AB\) and \(BC\) are perpendicular. Therefore \(ABCD\) is a rectangle.
- Find the coordinates of \(A\), \(B\), \(C\) and \(D\).
Since \(A\) lies on the \(y\)-axis, it lies at the \(y\)-intercept of \(y=2x+1\), which is \(1\). So \(A=(0,1)\).
Next, since \(C\) lies on the \(x\)-axis, which is \(y=0\), we can substitute this in to the equation of \(BC\) to find that \(x=12\), so \(C=(12,0)\).
To find the coordinates of \(B\), we must find where \(AB\) and \(BC\) meet, so we solve the simultaneous equations \(y=2x+1\) and \(2y+x=12\). Substituting the first into the second gives \[2(2x+1)+x=12,\] which gives us \(x=2\), so \(y=5\). Thus \(B=(2,5)\).
Now let’s find the coordinates of \(D\). To get from \(B\) to \(A\), we go left \(2\) and down \(4\), so we must do the same to get from \(C\) to \(D\), and so \(D=(10,-4)\).
In terms of vectors, the last sentence says: \(\overrightarrow{BA}=\overrightarrow{CD}=\dbinom{-2}{-4}\), so \(D=(10,-4)\).
- Find the area of \(ABCD\).

From the sketch, we can see (using Pythagoras’ theorem) that \(AB=\sqrt{2^2+4^2}=\sqrt{20}=2\sqrt{5}\).
Likewise, \(BC=\sqrt{5^2+10^2}=\sqrt{125}=5\sqrt{5}\).
Therefore the area of \(ABCD\) is \(AB\times BC=2\sqrt{5}\times 5\sqrt{5}=50\).

