Can we find the point midway between an intersection and a line?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let’s first find the coordinates of the point \(P\) by solving the simultaneous equations \(y+x=1\) and \(3y+2x=1\).

We can use substitution: we know that at \(P\), \(y=1-x\), so \[\begin{align*} &&3(1-x)+2x&=1,&&\quad \\ \implies&&3-3x+2x&=1,&& \\ \implies&&2&=x,&& \end{align*}\]

and so \(P\) is the point \((2,1-2)=(2,-1)\).

Alternatively, we could have used elimination: multiplying \(y+x=1\) by \(2\) gives the simultaneous equations \[\begin{align*} 2y+2x&=2\\ 3y+2x&=1. \end{align*}\]

Then either by subtracting these equations or by observation, we see that \(y=-1\), so \(x=2\), and \(P\) is the point \((2,-1)\).

Now let’s draw a diagram showing \(P\) and the line \(y=2x+8\).

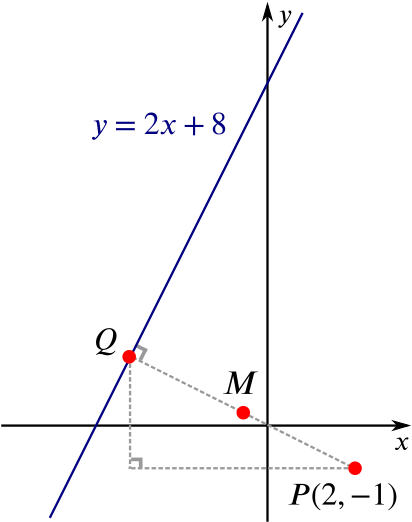
If we can find the line perpendicular to \(y=2x+8\) through \(P\), then we can find where these lines intersect, which we shall call \(Q\). We can then compute the coordinates of the point midway between \(Q\) and \(P\), which we shall call \(M\). This point \(M\) is the point the question has asked us to find.

A line perpendicular to \(y=2x+8\) must have gradient \(-\frac12\). Therefore the perpendicular passing through \(P(2,-1)\) has equation \[y+1=-\tfrac{1}{2}(x-2)\] (using the general formula \(y-y_1=m(x-x_1)\)), which we can rearrange to get \(y=-\frac12 x\).

So \(Q\) is the point of intersection of \(y=2x+8\) and \(y=-\frac{1}{2}x\). Solving these simultaneously, we find that \[-\tfrac{1}{2}x=2x+8,\] and so \(\frac{5}{2}x=-8\), giving \(x=-\frac{16}{5}\). Then we calculate \[y=-\frac{1}{2}\times\left(-\frac{16}{5}\right)=\frac{8}{5},\] therefore \(Q\) has coordinates \(\bigl(-\frac{16}{5},\frac{8}{5}\bigr)\).

The coordinates of \(M\) are the average (mean) of the coordinates of \(P\) and \(Q\). We therefore have \[\begin{align*} M&=\left(\frac{2+\bigl(-\frac{16}{5}\bigr)}{2},\frac{-1+\frac{8}{5}}{2}\right)\\ &=\left(\frac{\bigl(-\frac{6}{5}\bigr)}{2},\frac{\bigl(\frac{3}{5}\bigr)}{2}\right)\\ &=\left(-\frac{3}{5},\frac{3}{10}\right). \end{align*}\]