Here are some brief and informal notes on things that you might have noticed having tackled the questions suggested.
Given any three of the four equations that enclose a square, can you find the other one?
If we are given three equations we can solve them simultaneously to find the coordinates of their points of intersection. This would give us two of the four vertices of the square.
For the shape enclosed to be a square we know that there must be two pairs of parallel lines that intersect at right-angles. This tells us useful information about the gradients of the four lines.
Using the coordinates of two vertices we can find the side length of the square. This can be used to locate the third and fourth vertices and hence a fourth equation.
Three of the four equations are
\(y=3x+2\)
\(3y+x=8\)
\(3y+x=12\)
Find the fourth equation.
Find the area of the square.
Solving these three equations simultaneously gives us the coordinates of two vertices as \(\left(\frac{1}{5},\frac{13}{5}\right)\) and \(\left(\frac{3}{5},\frac{19}{5}\right)\).
If we now consider the diagram below, this gives us a fairly straightforward way of locating the third and fourth vertices.

Therefore, the third and fourth vertices could be located at \(\left(\frac{3}{5}+\frac{6}{5},\frac{19}{5}-\frac{2}{5}\right)\) and \(\left(\frac{1}{5}+\frac{6}{5},\frac{13}{5}-\frac{2}{5}\right)\).
This would give the fourth equation as \(y=3x-\frac{10}{5}\).
Alternatively, the third and fourth vertices could be located at \(\left(\frac{3}{5}-\frac{6}{5},\frac{19}{5}+\frac{2}{5}\right)\) and \(\left(\frac{1}{5}-\frac{6}{5},\frac{13}{5}+\frac{2}{5}\right)\).
This would give the fourth equation as \(y=3x+6\).
Using Pythagoras’ Theorem we can find the area of the square to be \(\frac{8}{5}\).
So if we are given three of the four equations enclosing a square, it is possible to find the area of the square but there are two possibilities for the fourth equation. There are two squares that exist, enclosed within the three given equations.
Can you see why there will always be two possibilities for the fourth equation?
You are given that the coordinates of two adjacent vertices of the square are \((\frac{1}{5},\frac{3}{5})\) and \((\frac{1}{5},-\frac{3}{5})\).
This problem is essentially the same as above. We can locate the third and fourth coordinates using the same method and hence find a fourth equation.
It is worth noting that once again there are two squares that exist, given the coordinates of these two adjacent vertices.
You are given the area of the square and the coordinates of one vertex. Can you find the equations?
Given the area of the square, we can immediately write down the side length. We now need to find a second vertex but without knowing the gradient of the side there are an infinite number of possible squares.
You are given that one vertex of a square is located at \((1,\frac{1}{5})\) and that one side adjacent to this vertex lies on the line \(5y=x\).
Can you describe a corresponding set of three equations that would enclose a square with an area of exactly 1?
We know that if the square has an area of exactly 1 then its side length must be 1. So, we need to find the coordinates of a point along the line \(5y=x\) a distance of 1 from \((1,\frac{1}{5})\).
There are two possible points like this. It may be helpful to use Pythagoras’ Theorem to form a quadratic equation in terms of \(a\) or \(b\).
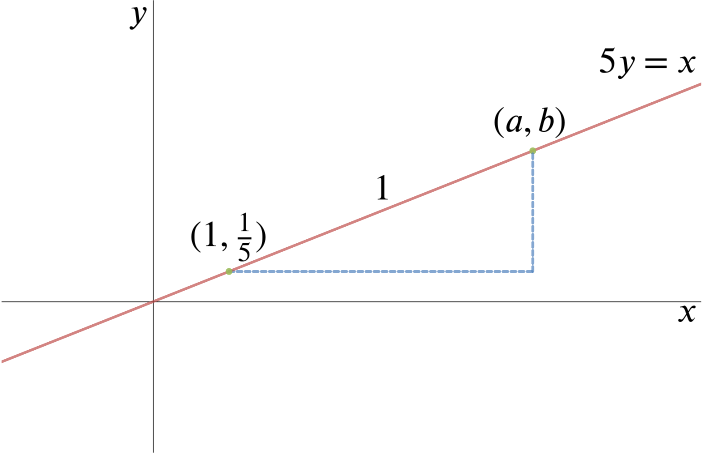
We know that \((a,b)\) lies on the line \(5y=x\) so we can write this coordinate as \((a, \frac{a}{5})\) or \((5b,b)\). The latter looks simpler to deal with so we’ll use that one.
We can express the base length of the right-angled triangle in the diagram as \(5b-1\) and the height of it as \(b-\frac{1}{5}\). Using Pythagoras’ Theorem we can then write \[(5b-1)^2+(b-\frac{1}{5})^2=1.\]
Expanding and simplifying this equation gives the quadratic \[26b^2-\frac{52}{5}b+\frac{1}{25}=0.\]
This gives the coordinates \((a,b)\) as \[\left(\frac{26\pm 5\sqrt{26}}{26},\frac{26\pm 5\sqrt{26}}{130}\right).\]
Once we have located a second vertex, the problem becomes the same as scenario 2.
What is a minimal amount of information needed to be able to describe the four equations enclosing the square?
Having explored the three scenarios highlighted in this problem you should have a better idea about the essential information required. One possibility is that we know something about the gradient of at least one side of the square and the side length of the square. The question is, how much of this information needs to be provided explicitly if we are to define a single square?
Another possibility is that we know the diagonal of the square, that is, the coordinates of two opposite vertices. If, for example, we know that two opposite vertices are at \((3,8)\) and \((7,1)\), can we determine the equations of the sides of the square?

