Given a function \(f\), the inverse of \(f\) is another function \(g\) with the property that \[g(f(x)) = x\] for every \(x\) in the domain of \(f\). If it is also true that \[f(g(x))=x\] for every \(x\) in the domain of \(g\) then the functions form a pair of inverses.
The inverse function for \(f\) is denoted by \(f^{-1}\). The function \(f\) has to be a bijection to possess an inverse. The domain of \(f^{-1}\) will be the range of \(f\) and vice versa.
For example:
If \(f(x) = x+a\), \(x\in\mathbb{R}\), then \(f^{-1}(x) = x-a\), \(x\in\mathbb{R}\).
The function \(f(x) = \cos x\), \(x\in\mathbb{R}\) has no inverse, as it is not bijective. However, the function \(f(x)=\cos x\), \(0\le x\le\pi\) has inverse \(f^{-1}(x) = \cos^{-1} x\), \(-1\le x\le1\).
If \(f(x) = e^x\), \(x\in\mathbb{R}\), then \(f^{-1}(x) = \ln x\), \(x\in\mathbb{R}\).
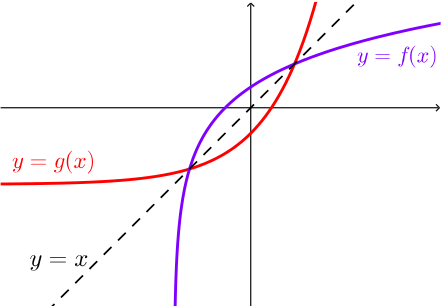
Note that the graph of \(y=f^{-1}(x)\) is a reflection of \(y=f(x)\) in the line \(y=x\).

