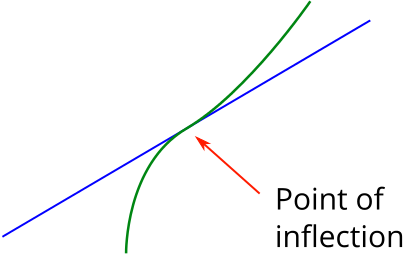
An inflection point, or point of inflection, is a point on a curve where the curve crosses its tangent at that point. For the graph of a function, another way of expressing this is that the second derivative is positive on one side of the point and negative on the other side.
For example, if \(y = x^3 + x^2 + x + 1\) then \(\dfrac{d^2 y}{dx^2} = 6x + 2\), which changes from negative to positive when \(x = - \frac{1}{3}\). Therefore \(y = x^3 + x^2 + x + 1\) has a point of inflection when \(x = - \frac{1}{3}\).
Some points to note:
A point of inflection may also be a stationary point, but it doesn’t have to be.
The second derivative will be zero at a point of inflection (if it is defined there).
If the second derivative is zero at a point, the point may or may not be a point of inflection.
More generally, a point of inflection on a curve is a place where the curvature changes from positive to negative or negative to positive. If you imagine walking along an \(S\)-shaped path, at some point you will change from turning to the left to turning to the right. This is a point of inflection.

