- The point with coordinates \((a,b)\), where \(a\) and \(b\) are rational numbers, is called:
an integer rational point if both \(a\) and \(b\) are integers;
a non-integer rational point if neither \(a\) nor \(b\) is an integer.
- Write down an integer rational point and a non-integer rational point on the circle \(x^2+y^2=1\).
An integer rational point? This is easy - \((0,1)\), for example.
A non-integer rational point? We can use Pythagoras’ Theorem, which tells us that a \(3-4-5\) triangle is right-angled.
Thus a \(3/5-4/5-1\) triangle is right-angled, and \(\left(\frac{3}{5},\frac{4}{5}\right)\) is a non-integer point on the circle.
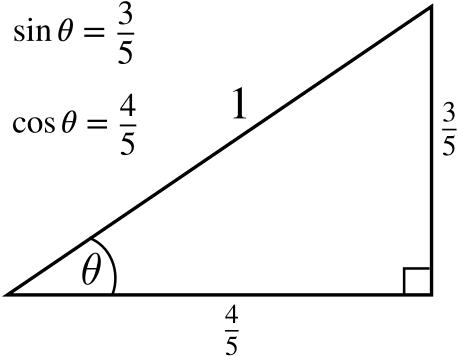
- Write down an integer rational point on the circle \(x^2+y^2=2\). Simplify \[(\cos\theta+\sqrt{m}\sin\theta)^2+(\sin\theta-\sqrt{m}\cos\theta)^2\] and hence obtain a non-integer rational point on the circle \(x^2+y^2=2\).
Once again, finding an integer rational point on the circle is easy: \((1,1)\), for example.
Multiplying out, we find that \[\begin{align*} (\cos\theta &+ \sqrt{m}\sin\theta)^2+(\sin\theta-\sqrt{m}\cos\theta)^2\\ &=\cos^2 \theta + 2\sqrt{m}\cos\theta\sin\theta+m\sin^2\theta+\sin^2\theta - 2\sqrt{m}\cos\theta\sin\theta + m\cos^2\theta\\ &=(1+m)\left(\cos^2\theta+\sin^2\theta\right)=1+m. \end{align*}\]So let’s put \(m=1\), and the above becomes \(\left(\cos\theta+\sin\theta\right)^2+\left(\sin\theta-\cos\theta\right)^2=2\), which looks like the equation of our circle. So the point \((x,y)=(\cos\theta +\sin\theta, \sin\theta-\cos\theta)\) must lie on the given circle.
So if we choose \(\theta\) to be the angle in the same \(3/5-4/5-1\) right-angled triangle as before, we find \[\begin{align*} x&=\cos\theta+\sin\theta = \frac{4}{5}+\frac{3}{5}=\frac{7}{5}\\ y&=\sin\theta-\cos\theta=\frac{3}{5}-\frac{4}{5}=-\frac{1}{5}. \end{align*}\]Check: \(\left(-\dfrac{1}{5}\right)^2+\left(\dfrac{7}{5}\right)^2 = 2\).
Thus a non-integer rational point on the circle \(x^2+y^2=2\) is \(\left(\frac{7}{5},-\frac{1}{5}\right)\).
- The point with coordinates \((p+\sqrt{2}q,r+\sqrt{2}s)\), where \(p\), \(q\), \(r\) and \(s\) are rational numbers, is called:
an integer \(2\)-rational point if all of \(p\), \(q\), \(r\) and \(s\) are integers;
a non-integer \(2\)-rational point if none of \(p\), \(q\), \(r\) and \(s\) is an integer.
- Write down an integer \(2\)-rational point, and obtain a non-integer \(2\)-rational point, on the circle \(x^2+y^2=3\).
This time we let \(m=2\). Thus \((\cos\theta+\sqrt{2}\sin\theta)^2+(\sin\theta-\sqrt{2}\cos\theta)^2\) is on the circle \(x^2+y^2=3\).
Setting \(\theta=0\) we find \((1,-\sqrt{2})\), an example of an integer \(2\)-rational point.
Using \(\cos\theta=\dfrac{4}{5},\,\sin\theta=\dfrac{3}{5}\) (as before) we find the non-integer \(2\)-rational point \[\left(\frac{4}{5}+\frac{3}{5}\sqrt{2},\frac{3}{5}-\frac{4}{5}\sqrt{2}\right).\]
Check: \(\left(\dfrac{4}{5}+\dfrac{3}{5}\sqrt{2}\right)^2+\left(\dfrac{3}{5}-\dfrac{4}{5}\sqrt{2}\right)^2=3.\)
- Obtain a non-integer \(2\)-rational point on the circle \(x^2+y^2=11\).
Note that \(x^2 + y^2=11=1+10\) and we want a \(\sqrt{2}\) rather than a \(\sqrt{10}\), so some scaling is required.
so taking the same values for \(\cos\theta\) and \(\sin\theta\) as before we find an example of a non-integer 2-rational point on the circle \(x^2+y^2=3\): \[\left(\frac{12}{5}+\frac{3}{5}\sqrt{2},\frac{9}{5}-\frac{4}{5}\sqrt{2}\right).\]
- Obtain a non-integer \(2\)-rational point on the hyperbola \(x^2-y^2=7\).
There are few different ways to approach this. Here are three. Note that in all three we have a certain amount of freedom in how we choose our numbers.
Approach 1—Simple algebra
We know that if \((p+\sqrt{2}q, r+\sqrt{2s})\) lies on the hyperbola \(x^2 - y^2 = 7\), then \[p^2 + 2q^2 - r^2 -2s^2 + 2\sqrt{2}(pq - rs)=7.\]
Thus we could sensibly choose \(p^2 + 2q^2 - r^2 - 2s^2=7, \quad pq - rs=0.\)
The second equation here suggests putting \(p =ks, r = kq\), whereupon the first equation becomes \((k^2-2)(s^2-q^2) = 7\).
Now \(k = 3\) is the obvious choice, giving \(s^2 - q^2 = 1\), which yields \((s+q)(s-q) = 1\).
Putting \(s+q = 2\) and \(s-q = \dfrac{1}{2}\) gives \(s = \dfrac{5}{4}, q = \dfrac{3}{4}\), and thus \(p = \dfrac{15}{4}, r = \dfrac{9}{4}\).
Thus \(\left(\dfrac{15}{4} + \sqrt{2}\dfrac{3}{4}, \dfrac{9}{4}+ \sqrt{2}\dfrac{5}{4}\right)\) is our non-integer 2-rational point, as required.
Approach 2—Trigonometry
Instead of the identity \(\cos^2 \theta+\sin^2\theta=1\), we instead use \(\sec^2\theta-\tan^2\theta=1\). We therefore try \[\begin{align*} x&=e\sec\theta+f\sqrt{m}\tan\theta\\ y&=e\tan\theta+f\sqrt{m}\sec\theta.\\ \end{align*}\]Then \[x^2-y^2=e^2-f^2m.\] As before, \(m=2\) so we can make \(7\) with the integers \(e=3\) and \(f=1\). Then \[(x,y)=(3\sec\theta+\sqrt{2}\tan\theta,3\tan\theta+\sqrt{2}\sec\theta).\] Using \(\cos\theta=\dfrac{4}{5}\) and \(\sin\theta=\dfrac{3}{5}\) again, we find \(\sec\theta=\dfrac{5}{4}\) and \(\tan\theta=\dfrac{3}{4}\) and so we have \[(x,y)=\left(\frac{15}{4} + \frac{3}{4}\sqrt{2}, \frac{9}{4}+\frac{5}{4}\sqrt{2}\right).\]
Approach 3—Hyperbolic functions
We can also approach this problem using the hyperbolic functions, which makes sense as \(x^2-y^2=7\) is a hyperbola. Note the identity \[\cosh^2\theta-\sinh^2\theta=1,\] so try \[\begin{align*} x&=e\cosh\theta+f\sqrt{m}\sinh\theta\\ y&=e\sinh\theta+f\sqrt{m}\cosh\theta.\\ \end{align*}\] Then \[x^2-y^2=e^2-f^2m.\] As before, \(m=2\) so we can make \(7\) with the integers \(e=3\) and \(f=1\). Then \[(x,y)=(3\cosh\theta+\sqrt{2}\sinh\theta,3\sinh\theta+\sqrt{2}\cosh\theta).\] Then exploiting the definitions of \(\cosh\) and \(\sinh\) we have \[\cosh\theta=\frac{e^{\theta}+e^{-\theta}}{2} \qquad \qquad \sinh\theta=\frac{e^{\theta}-e^{-\theta}}{2}.\] We can take \(\theta=\log 2\) to find an example of a non-integer \(2\)-rational point: \[\begin{align*} \cosh(\log 2)&=\frac{e^{\log 2}+e^{-\log 2}}{2}=\frac{2+\frac{1}{2}}{2}=\frac{5}{4}\\ \sinh(\log 2)&=\frac{2-\frac{1}{2}}{2}=\frac{3}{4} \end{align*}\]and so we obtain \[(x,y)=\left(\frac{15}{4} + \frac{3}{4}\sqrt{2},\frac{9}{4}+\frac{5}{4}\sqrt{2}\right).\]

