This applet shows the graph of the parabola \(y=\dfrac{x^2}{4a}\) with its focus \(F\) at \((0,a)\). The value of \(a\) can be changed by sliding the left slider.
The parabola can be rolled along the \(x\)-axis by moving the right slider.
As we roll the parabola in this way, what is the (cartesian equation of the) locus of the focus \(F\)?
Can you find the coordinates of a general point \(P\) on the parabola?
What do you think would be the most useful form to give the coordinates in?
An obvious answer is that the coordinates of \(P\) are just \((x, \frac{x^2}{4a})\), using the equation of the parabola.
However, experience with conics (ellipses, parabolae and hyperbolae) suggests that things will be easier if we use parametric coordinates.
For the parabola \(y^2=4ax\), the standard parametrisation is \((at^2, 2at)\). Our parabola, however, has \(x\) and \(y\) switched, so that its equation is \(x^2=4ay\); therefore the parametric coordinates of \(P\) are \((2at, at^2)\).
Instead of the parabola rolling, how else could you think about the scenario?
The parabola rolling on the \(x\)-axis means that the \(x\)-axis is always tangent to the rolled parabola.
So an alternative way to think about this is to draw a tangent to the parabola and work out distances in relation to this tangent, as we have done in this image:
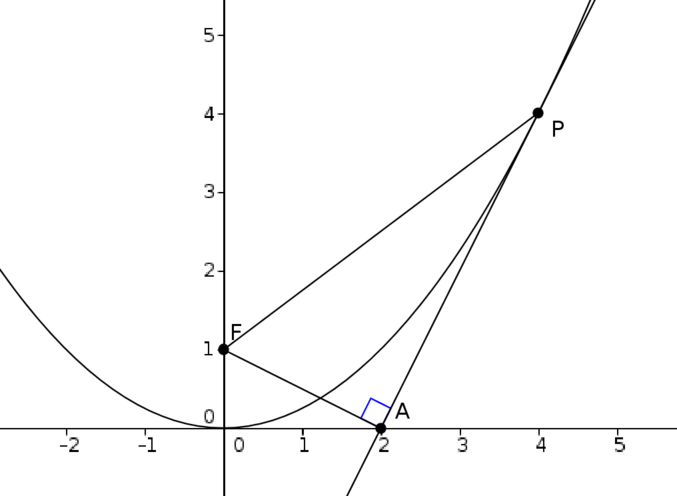
The tangent is drawn from \(P\), and a perpendicular is dropped from \(F\) to the tangent, meeting the tangent at \(A\). Then if we know that the point \(P\) ends up at \(P'=(x',0)\) on the \(x\)-axis, the \(x\)-coordinate of the focus will be \(x'-PA\) and the \(y\)-coordinate will be \(AF\).
What is the equation of the tangent through the point \(P\)?
(If you found different forms of the point \(P\) in mini-question 1 which is most useful?)
We differentiate the equation \(y=\dfrac{x^2}{4a}\) to get \(\dfrac{dy}{dx}=\dfrac{x}{2a}\).
Then at the point \(P(2at, at^2)\), we have \(\dfrac{dy}{dx}=\dfrac{2at}{2a}=t\).
We can now write down the equation of the tangent: it is \[y-at^2=t(x-2at)\] which we can rearrange to \[y=tx-at^2.\]
It appears in the diagram above that the point \(A\) (the foot of the perpendicular from \(F\) to the tangent through \(P\)) lies on the \(x\)-axis.
Is this actually the case, and if so, does it always happen, or does it only occur for certain choices of \(P\)?
What angle does the tangent make with the \(x\)-axis?
If the tangent makes an angle of \(\theta\) with the \(x\)-axis, then \(\tan\theta=\dfrac{dy}{dx}=t\), so \(\theta=\arctan t\).
What is the angle between \(PF\) and the tangent to the parabola at \(P\)? (Is there a nice way to work this out?)
If we draw in the vertical through \(P\), as in the following diagram, we might be reminded of the focal property of parabolas: rays of light parallel to the axis of symmetry reflect off the parabola and then pass through the focus.
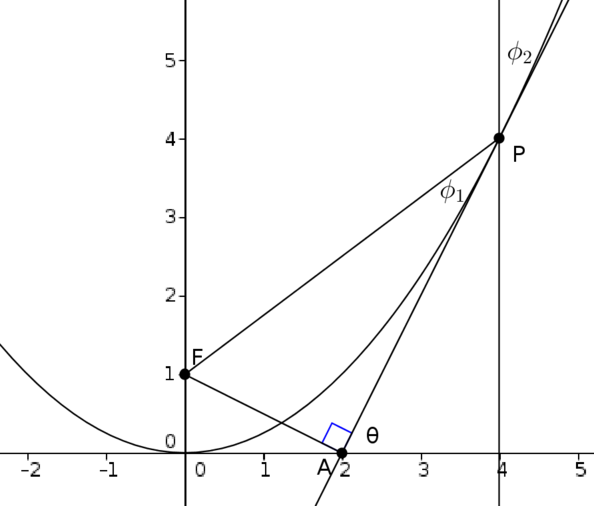
So the two angles marked in the diagram, \(\phi_1\) (between the tangent and \(PF\)) and \(\phi_2\) (between the tangent and the vertical) are equal.
But \(\phi_2=\frac{\pi}{2}-\theta\) as the tangent makes an angle of \(\theta\) with the horizontal.
Thus the angle we want, \(\phi_1=\frac{\pi}{2}-\theta=\frac{\pi}{2}-\arctan t= \arctan(1/t)\).
This also shows that \(\angle PFA=\theta=\arctan t\).
If we are able to show that \(A\) lies on the \(x\)-axis, then this also shows that there are three similar right-angled triangles in the diagram: \(FAP\), \(AMP\) (where \(M\) is the point where the vertical through \(P\) meets the \(x\)-axis) and \(FOA\). This observation might be useful later on. It’s always worth keeping an eye out for similar triangles!
When the parabola has rolled so that the point \(P\) lies on the \(x\)-axis, what are the coordinates of the new location of \(P\)?
So the new location of \(P\) is \(\bigl(a(\arsinh t+t\sqrt{1+t^2}), 0\bigr)\).
Can you put all of your answers together to now work out the coordinates of the focus \(F\) when \(P\) lies on the \(x\)-axis?
As we explained above, we need to find the lengths \(PA\) and \(AF\) to calculate the new coordinates of the focus. There are several different ways to achieve this; here is one of them which does not require us to determine whether \(A\) lies on the \(x\)-axis.
We know the original coordinates of \(F(0,a)\) and \(P(2at,at^2)\), so we can calculate the length \(FP\) as \[\begin{align*} FP&=\sqrt{(2at)^2+(at^2-a)^2}\\ &=a\sqrt{4t^2+t^4-2t^2+1}\\ &=a\sqrt{t^4+2t^2+1}\\ &=a(1+t^2) \end{align*}\]Alternatively, we can use the focus-directrix property of the parabola: \(FP\) equals the distance of \(P\) from the directrix \(y=-a\), which is clearly \(at^2+a\).
Now, we know that \(\angle PFA=\theta=\arctan t\), so \(\sin\theta=\dfrac{t}{\sqrt{1+t^2}}\) and \(\cos\theta=\dfrac{1}{\sqrt{1+t^2}}\). Therefore \[PA=FP\sin\theta=a(1+t^2)\times\frac{t}{\sqrt{1+t^2}}=at\sqrt{1+t^2}\] and \[FA=FP\cos\theta=a(1+t^2)\times\frac{1}{\sqrt{1+t^2}}=a\sqrt{1+t^2}.\]
Therefore the new coordinates of the focus are \[\bigl(a(\arsinh t+t\sqrt{1+t^2}) - at\sqrt{1+t^2}, a\sqrt{1+t^2}\bigr) = \bigl(a\arsinh t, a\sqrt{1+t^2}\bigr).\]
Incidentally, as the angle between \(FA\) and the \(y\)-axis is \(\theta\), it follows that the \(y\)-coordinate of \(A\) is \[a-FA\cos\theta = a - a\sqrt{1+t^2}\times\frac{1}{\sqrt{1+t^2}}=0,\] so \(A\) does, indeed, lie on the \(x\)-axis.
A simpler argument for the same result is as follows. From the equation of the tangent (see the solution to mini-question 3 above), we deduce that the tangent meets the \(x\)-axis at \(B\) which has coordinates \((at,0)\). Then \(FB\) has gradient \(\frac{-a}{at}=-\frac{1}{t}\), so \(FB\) is perpendicular to the tangent, so \(B\) and \(A\) are the same point.
There are also other ways to deduce this which are more geometric in nature and use the focus-directrix property of the parabola.
This should give you enough to find the cartesian equation of the locus!
The new coordinates of the focus are \[x=a\arsinh t, \quad y=a\sqrt{1+t^2}\] So \(t=\sinh(x/a)\), which we can substitute into the equation for \(y\) to get \[y=a\sqrt{1+\sinh^2\bigl(\frac{x}{a}\bigr)}= a\sqrt{\cosh^2\bigl(\frac{x}{a}\bigr)}=a\cosh\frac{x}{a},\] which is the equation of a catenary!

